Geometria analityczna Ewkaa: Hej Punkty A(0, −5) oraz D(−3,−1) są kolejnymi wierzchołkami trapezu równoramiennego ABCD, którego osią symetrii jest prosta o równaniu x+2y=0. Oblicz współrzędne pozostałych wierzchołków oraz długość odcinka łączącego środki ramion tego trapezu. Nie mam totalnie żadnego pomysłu. Proszę o pomoc; z góry dziękuję.

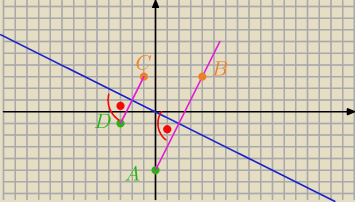
Qulka: B(4,3) C(−1,3)

Ewkaa: super jak to policzyć?

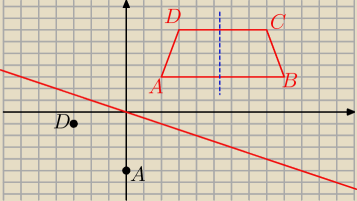
Antonni: Czym jest os symetrii takiego trapezu ? Wyznacz wiec punkty symetryczne do A i do D wzledem tej prostej i masz wspolrzedne pozostalych punktow

	AB+CD
DLugosc odcinka laczacego srodki bokow to
	2

Masz juz wszytko do pilczenia

Qulka: prostopadła do niebieskiej przechodząca przez A ..i potem odległość Aniebieska =Bniebieska

Ewkaa: ok. dziękuję

Antonni: Obliczmy wspolrzedne punktu C os symetrii ma rownanie y=−0,5x To prosta prostopadla do niej bedzie miala wspolczynnik kierunkowy a=2 Prosta prostopadla i przechodzaca przez punkt D=(−3,−1) bedzie miala rownaie y₁ = a(x−x₀)+y₀ y₁= 2(x+3)−1 y₁= 2x+6−1= 2x+5 Liczymy punkt przecia sie tych prostych −05x=2x+5 −2,5x=5 to x=−2 y= −0,5x to y=1 Oznaczmy go jako S=(−2,1) Bedzie to srodek odcinka DC Teraz ze wzoru na srodek odcinka policzmy wspolrzedne punktu C

	xD+xC
xs=
	2

2x_s= x_d+x_c x_C= 2x_s−x_D x_c= 2*(−2)−(−3)= −4+3= −1`

	yd+yc
yS=
	2

y_c= 2*y_s−y_d y_c= 2*1+1=3 C=(−1,3) =========== Tak samo policz wspolrzedne punktu B Moze mozna prosciej (ja to zrobilem tak