Geometria analityczna Ewkaa: Hej Punkty A(2, −3) i B(5, 1) są wierzchołkami trójkąta ABC. Bok BC zawiera się w prostej k: x+2y−7=0, zaś środkowa AM zawiera się w prostej m: 5x−y−13=0. Wyznacz równanie ogólne prostej, w której zawiera się wysokość trójkąta poprowadzona z wierzchołka C. No więc; na razie znalazłam punkt wspólny prostej BC i AM => M(3, 2). Korzystając z wiedzy, że środek odcinka to średnia arytmetyczna współrzędnych wyznaczających początek i koniec obliczyłam wierzchołek C(1, 3). Następnie wyznaczyłam wzór prostej AB: 4x−7y−29=0. Potem odległość punktu C od prostej AB = ^46√65₆₅. Serio nie wiem jak to obliczyć dalej. W sumie nie wiem też, czy moje obliczenia są poprawne... Z góry dziękuję za pomoc

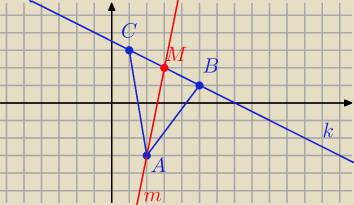Janek191: Wyznacz prostą AB , a następnie prostą do niej prostopadłą przechodzącą przez C.

Ewkaa: Dobra wiem xp w sensie odległość punktu od prostej była niepotrzebna − hc jest prostopadłe do AB więc wszystko dalej obliczyłam. Problem jest taki, że wyszło mi 7x+4y−19=0, a powinno... 3x+4y−15=0 Gdzie jest błąd?

Ewkaa: ooo... dzięki masz może pomysł gdzie się machnęłam?

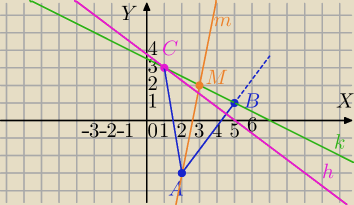Mila: A(2, −3) i B(5, 1)

	1		7
k: x+2y−7=0,⇔y=−		x+
	2		2

m: 5x−y−13=0⇔y=5x−13 M=(3,2) Mjest środkiem BC BM^→[−2,1] M=(3,2)→T_[−2,1]=C=(3+(−2),2+1)=(1,3) AB: −3=2a+b 1=5a+b −4=−3a

	4
a=		współczynnik kierunkowy prostej AB
	3

b=−5²₃

	4
AB: y=		x−523
	3

h: h⊥AB i C∊h

	3		3
y=−		x+b , 3=−		*1+b⇔b=334
	4		4

	3
h: y=−		x+334 równanie kierunkowe
	4

4y=−3x+15 3x+4y−15=0 równanie ogólne

Ewkaa: Dziękuję zrobiłam mały obliczeniowy. Dzięki bardzo

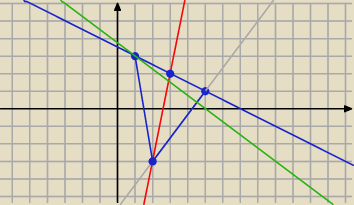Janek191: x + 2y − 7 = 0 5 x − y − 13 = 0 ⇒ y = 5 x − 13 −−−−−−−−−−− x + 2*( 5 x − 13) − 7 = 0 11 x − 33 = 0 x = 3 === y = 2 ==== M = ( 3, 2) ======== B = ( 5, 1)

a + 5		b + 1
	= 3		= 2
2		2

a + 5 = 6 b + 1 = 4 a = 1 b = 3 C = ( 1, 3) ======== A = ( 2, − 3) B = ( 5, 1)

	1 − (−3)		4
		=
	5 − 2)		3

Pr. AB

	4
y =		x + b
	3

	4
− 3 =		*2 + b
	3

	9		8
−		−		= b
	3		3

	17
b = −
	3

	4		17
y =		x −
	3		3

============= Prosta prostopadła

	3
y = −		x + b1 C = ( 1, 3)
	4

	3
3 = −		*1 + b1
	4

	3		15
b1 = U{12]{4} +		=
	4		4

	3		15
y = −		x +		/ * 4
	4		4

4 y = − 3 x + 15 3 x + 4 y −15 = 0 ============

Ewkaa: dziękuję.