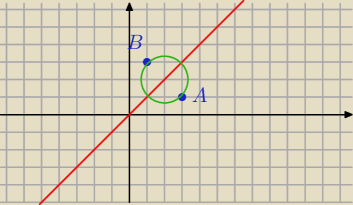
gee aaaa: napisz nierównosc opisującą koło którego środek należy do prostej y=x a punkty A=(3,1) B=(1,3) należa do brzegu koła narysowałem i wyszło ze y=x jest symetralna tych odcinka AB wiec jest nieskonczenie wiele takich kół jak wiec zapisac taką nierównosc? wytłumaczy ktos?

Jack:

Adamm: (x−a)²+(y−a)²=(√(a−1)²+(a−3)²)²

Jack: Prosta AB :

	3−1
a =		= − 1
	1−3

y = −1(x−3)+1 = −x + 4 Przeciecie sie prostej AB z prosta y=x −x+4 = x 2x = 4 −>> x = 2 y = 2 Zatem srodek okregu ma wspolrzedne S(2,2) odleglosc punktu A od prostej y = x :

	|3 − 1|
d =
	√2

	2
d =		= √2
	√2

r − promien okregu = (√2)² = 2 Zatem rownanie okregu to (x−2)²+(y−2)² = 4

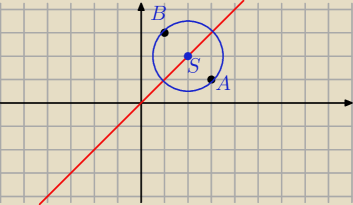
5-latek: Punkt A jest symetryczny wzgledem prostej y=x WObec tego policz wspolrzedne srodka S Odleglosc punktu A od prostej y=x to promien tego kola POtem napisz nierownosc (x−x_s)²+(y−y_s)≤r²

aaaa: Jack tak zrobilem, ale to jest jedno z mozliwych rozwiazac bo przeciez srodek rownie dobrze moze byc gdzie indziej i wlasnie musze napisac nierownosc ktora sie sprawdzi dla kazdego przypadku i niewiem jak to zrobic

Adamm: aaaa patrz na wypowiedź 5−latka

aaaa: tak jak wy mowicie to to sam rozwiazalem ale w odpowiedziach mam (x−a)²+(y−a)² ≤ 2a²−8a+10, a nalezy do R

Adamm: zamień znak równośći w moim na ≤ i masz to samo