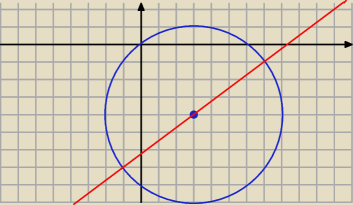
geee aaaa: Napisz równanie prostej przechodzącej przez środek okręgu (x−3)²+(y+4)²=25 i środek cięciwy AB tego okręgu zawartej w prostej 3x−4y−25=0. z tego S=(3,−4)

	4
a prostej prostopadej = −
	3

	4
y=−		x+b
	3

	4
−4=−		*3+b
	3

−4=−4+b b=0

	4
y=−		x
	3

wydaje mi sie ze o to chodzi a dlaczego w odpowiedziach jest y=ax−4−3a, a nalezy do R

Adamm: prosta 3x−4y−25=0 przecina punkt S

Adamm: dlatego każda prosta która przecina punkt S jest daną prostą

Adamm: inaczej, środek cięciwy to środek okręgu

Jack:

aaaa: a jak napisac rówanie dowolnej prostej przechodzacej przez tylko jeden punkt np w tym przypadku przez S? bo nieogarniam jak dojsc do tego y=ax−4−3a

Adamm: y=ax+b wstawiamy punkt (3;−4) −4=3a+b b=−4−3a y=ax−4−3a