wartosc bezwzgledna
Patyczak: |2x−1|=2x−1 co to tutaj trzeba zrobić
1 paź 10:44
Omikron: Zdejmij moduł w dwóch przedziałach.
1) x∊(−∞,1/2)
2) x∊<1/2,∞)
W każdym rozwiąż równanie.
1 paź 10:46
Patyczak: | | 1 | |
dzieki w jednym wyszło x= |
| a w drugim tożsamość |
| | 2 | |
1 paź 10:51
Patyczak: dobrze

1 paź 10:51
Omikron: Tak.
1 paź 10:57
Omikron: Przy czym w pierwszym przedziale 1/2 odpada, bo nie należy do dziedziny, ale wchodzi w drugim
przedziale.
1 paź 10:58
Antonni: Nalezy skorzystac z definicji wartosci bezwzgleednej
|x|= x dla x≥0
|x|= −x dla x<0
Tutaj masz ze |x|=x wiec beda rozwiazania dla 2x−1≥0
A dla jakich xow bedzie
|2x−1|= 1−2x?
1 paź 11:00
Patyczak: |a|=−a ⇔ a≤0
1 paź 11:08
1 paź 11:08
Antonni: Zastosuj poprawnie definjcje
jesli dla |x|=x dla x≥0 to |x|=−x dla x<0
Popraw i bierz nastepne zadanie
1 paź 11:11
Antonni: jesli uczysz sie do matury to w ramach cwiczenia
Narysuj wykres funkcji f(x)= |2−3x|+|x+3|
1 paź 11:16
Antonni: Nastepne
czy potrafisz stwierdzic od razu ( bez rozwiazywania) takiego rownania ze to rownanie nie ma
rozwiazn (jest sprzeczne
|x+3|+|x−1|=3 ?
1 paź 11:20
Patyczak:
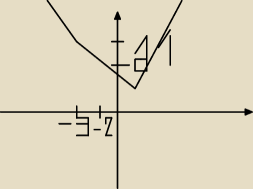
rozbijamy na 3 przedzialy
I x∊(−
∞,−3)
2−3x−x−3=y
−4x−1=y
2−3x+x+3=y
y=−2x+5
−2+3x+x+3=y
y=4x+1
1 paź 11:26
Antonni: Dobrze .
1 paź 11:30
Patyczak: to drugie wiem o co chodzi ale nie moge tego wytłumaczyć
po prostu jak podstawimy dowolną liczbę rzeczywistą pod x to nie da nam ona tej liczby 3
np
podstawiamy 0
3−1=3
podstawiamy 1
4 + 0 =3
w kazdym wyjdzie sprzeczność
1 paź 11:32
Antonni: Korzystamy z tego ze |x|= |−x|
|x+3|+|x−1|=|(x+3)+(1−x)|≠3
1 paź 11:39
Patyczak:

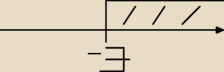
Na rysunku przedstawiony jest zbiór wszystkich liczb rzeczywistych spełniających nierówność
|2x−8|≤10
stąd wynika , że:
A)k=2
B)k=4
C)k=5
D)k=9
1 paź 11:42
Patyczak: wiem , średnią arytmetyczną jego końców jest 4 ale co dalej?
1 paź 11:43
Omikron: Rozwiąż nierówność po prostu.
1 paź 11:45
Ajtek:
Przesuń się od 4 o pięć w prawo

1 paź 11:46
Patyczak: ok wyszlo x∊<−1,9>
czyli k=9
1 paź 11:47
Omikron: Dobrze
1 paź 11:47
Antonni: WIdze ze jestes rozgarniety i nie trolujesz to w takim razie takie zadanie
Rozwiaz rownanie i zaznacz rozwiazanie na osi liczbowej
√9+6x+x2=x+3
√2−√24*x+3x2= √2−√3*x
Podobne do zadania 1 tylko musisz wykorzystac znany wzor tutaj
1 paź 11:57
Patyczak:
1)
√(x+3)2=x+3
|x+3|=x+3
x+3 ≥ 0
x ≥ −3
x∊<−3,+
∞)
2)
√2−2√6x+3x2=
√2−
√3x
√(−√3x+√2)2=
√2−
√3x
|
√2−
√3x|=
√2−
√3x
√2−
√3x ≥ 0
√3x ≥
√2
dobrze?
1 paź 12:09
Antonni: Wedlug mnie 1 dobrze
Natomiast nr2 o ile √2−2√6+3x2= √(√2−√3*x)2= √2−√3x dla x≥0 to juz
rozwiazanie tej nierownosci nie .
zapomniales o czyms .
1 paź 12:19
Patyczak: teraz chyba dobrze
1 paź 12:22
Antonni: Dobrze .
ja juz musze robic swoje zadania a Ty sobie rozwiaz takie rownanie
|x+1|−|x|+3|x−1|−2|x−2|= x+2
1 paź 12:27
szkapa: x∊{−2}u<2,+∞)
1 paź 12:36
patyczak: rozwiazane
1 paź 12:38

 rozbijamy na 3 przedzialy
I x∊(−∞,−3)
2−3x−x−3=y
−4x−1=y
rozbijamy na 3 przedzialy
I x∊(−∞,−3)
2−3x−x−3=y
−4x−1=y
 Na rysunku przedstawiony jest zbiór wszystkich liczb rzeczywistych spełniających nierówność
|2x−8|≤10
stąd wynika , że:
A)k=2
B)k=4
C)k=5
D)k=9
Na rysunku przedstawiony jest zbiór wszystkich liczb rzeczywistych spełniających nierówność
|2x−8|≤10
stąd wynika , że:
A)k=2
B)k=4
C)k=5
D)k=9

 1)
√(x+3)2=x+3
|x+3|=x+3
x+3 ≥ 0
x ≥ −3
x∊<−3,+∞)
2)√2−2√6x+3x2=√2−√3x
√(−√3x+√2)2=√2−√3x
|√2−√3x|=√2−√3x
√2−√3x ≥ 0
√3x ≥ √2
1)
√(x+3)2=x+3
|x+3|=x+3
x+3 ≥ 0
x ≥ −3
x∊<−3,+∞)
2)√2−2√6x+3x2=√2−√3x
√(−√3x+√2)2=√2−√3x
|√2−√3x|=√2−√3x
√2−√3x ≥ 0
√3x ≥ √2