Zespolone Jack: Zespolone (argument liczby zespolonej) Podaj geometryczna interpretacje zbiorow liczb zespolonych d)

	z+1		π
arg		=
	z−1		2

Po pierwsze − czy moge to tak przeksztalcic?

	z+1		z−1 + 2		2
arg		= arg		= arg(1 +		)
	z−1		z−1		z−1

tylko co dalej?

jc: Jak policzysz moduł liczby (z+1)/(z−1), zobaczysz rozwiązanie.

Jack: jc 1) dlaczego tak 2) jak policzyc modul z dzielenia?

jc: A może trzeba inaczej. Liczba o argumencie π/2 ma postać ti, t > 0. (z+1)/(z−1)=ti Wylicz zet i będziesz miał rozwiązanie.

jc: Moduł ilorazu to iloraz modułów, ale to była fałszywa wskazówka Drugi wpis daje rozwiązanie. Na pewno to jakaś półprosta.

Jack:

2
	= ti − 1
z−1

	2
z−1 =
	ti − 1

	2
z =		+ 1
	t−1

jednakze nie wiem co nam to daje, skoro mam to narysowac.

jc: z+1 = (z−1) ti ti + 1 = z (ti − 1) z= (ti + 1) / (ti − 1) |z| = 1, to jest fragment okręgu o promieniu 1. Jaki fragment?

Jack: |z| = |x+iy| = √x²+y² sadzilem ze to jest po prostu okrag, a nie jego fragment...

jc: Dla t = 0 mamy −1, dla t =∞ mamy 1. Czy to będzie dolna część czy górna? Wystarczy podstawić t = 1. (i+1)/(i−1)=−i, a więc dół. Nie podoba mi się to ... Lepiej sprawdź.

Jack: naprawde nie rozumiem co masz na mysli. pierwszy raz robie jakiekolwiek tego typu zadanie. Poszukam w zbiorze moze cos bedzie...

Jack: jc Przepraszam jesli zabrzmialo to troche pejoratywnie. Doceniam starania ale niestety nic mi nie wyjasniaja. Znalazlem taki wzor :

	z1
arg(		) = arg z1 − argz2 + 2kπ
	z2

to moze oto chodzi ? wtedy

	π
arg(z+1) − arg(z−1) + 2kπ =
	2

Chociaz to mi tez nic nie mowi. Byc moze teraz moduly nalezy obliczyc?

jc: Dla różnych wartości t, otrzymujesz różne punkty na okręgu. Wszystkich jednak nie otrzymasz. z=x+iy. Wylicz x i y. Przyjrzyj się jaki fragment okręgu otrzymasz.

Jack: czyli innymi slowy − post 11:16 jest kompletnie bezuzyteczny, wracamy do

	ti + 1
z =
	ti − 1

i teraz tu podstawic x + iy?

jc: No dobrze, po kolei.

	z+1		z+1
arg		= π/2 oznacza, że liczba		leży na górnej części osi pionowej.
	z−1		z−1

z+1
	= ti, t > 0.
z−1

Wyliczasz z tego równania z.

	ti + 1
z =
	ti − 1

Możesz od razu stwierdzić, że moduł licznika = moduł mianownika = √1+t². Zatem moduł ilorazu wynosi 1, |z| = 1. Wiemy więc, że dla każdego t, punkt z leży na okręgu o środku 0 i promieniu 1. Podstawiając różne dodatnie wartości t, nie uzyskasz wszystkich punktów okręgu.

jc: Tak, dwa wpisy były bez sensu. Ten o liczeniu modułu oraz ten z sugestią, że to prosta

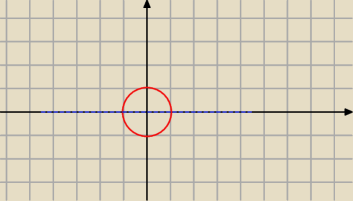
Jack: To jest jasne do momentu, ze nie uzyskam wszystkich punktow okregu. Pytanie dlaczego skoro mam x²+y² = 1... Chyba, ze chodzi o to : Na poczatku mielismy, ze t>0, zatem patrzymy na niebieska linie przerywana i od niej do gory.

jc:

	1 + i tg α/2
Wykonaj rachunek		. Zobaczysz więcej.
	1 − i tg α/2

Jack:

	α   (1+ i tg )2   2
... =		=
	α   1 + tg2   2

	α   α   1 + i 2 tg − tg2   2   2
=		= yyyy?
	α   1 + tg2   2

apropo, skad to rownanie?

Jack: dobra, juz chyba wiem

	α   α   1 − tg2 + i 2 tg   2   2
... =		=
	α   1 + tg2   2

	α   1 − tg2   2		α   i 2 tg   2
=		+		=
	α   1 + tg2   2		α   1 + tg2   2

= cos(α) + i sin(α)

jc: W zadaniu t = tg α/2, t > 0, czyli α > 0. Przed wszystkim trzeba jednak postawić minus (porównaj mianowniki). Przy okazji wyraziłeś sin α i cos α przez t = tg α/2. Przydaje się przy całkowaniu. Ale teraz, w czasach, kiedy mam dostęp do systemów algebry komputerowej nie ma to większego znaczenia (mam na myśli umiejętność całkowania).

Jack: teraz musze leciec, bede wieczorem to moze po kontynuujemy ten temat, poki co − nadal srednio to widze.

jc: Ja kiedyś do tego wrócisz, zobaczysz wynik bez liczenia. Teraz wyjeżdżam na kilka dni.

Jack: hmm, no to pomysle nad tym jeszcze troche.