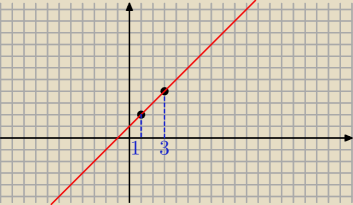
Wykresy Antonni: Wyznacz liczby a,b c d tak aby wykres funkcji f(x)= |ax+b|+|cx+d| x∊R byl suma odcinka AB gdzie A=(1,2) i B= (3,4) A∉prostej BD i B∉do prostej AC Sporzad wykres Jedynie co moge zapisac to rownanie prostej przechodzacej przez punkty A i B Bedzie to rownanie postaci f(x) = 1(x−1)+2=x+1 dla x∊<1,3) To zostaly by jeszce dwa przedzialy do rozpatrzenia 1x∊(−∞,1) 3. x∊<3,∞) A tutaj juz nie wiem jak

Qulka: może |2x−2|+|x−3|

Antonni: Mam zapisane tak f(x)= −3x+5 dla x<1 f(x)= x+1 dla 1≤x<3 f(x)= 3x−5 dla 3≤x To tak Qulka na szybkiego zgadzaloby sie .

Qulka: wymyśliłam że w tych punktach muszą być miejsca zerowe i tak wyszło

Mila: Coś ta treść mi się nie podoba. Chyba nie dokończyłeś.

Antonni: Mila jest to czesc zadania ktorego tresc jest taka A) Sporzad wykres funkcji f(x)=|2−3x|+|x+3| B) Funkcje f(x)= |ax|b|+|cx+d| x∊R okresl za pomoca wzorow postaci f(x)= mx+n Zakladamy ze

b		d
	>		i a>0 ic>0
a		c

Te podpunkty zrobilem To jest podpunkt nr C) do tego zadania z ktorym sobie nie moge poradzic

Antonni: ma byc |ax+b|

Antonni: Qulka Rzuc pomyslem jak wymyslilas?

Qulka: skoro A∉prostej BD i B∉do prostej AC to zrobiłam miejsca zerowe w 1 i 3 i wybrałam najprostszy mnożnik żeby nie było płaskie czyli a=2

Antonni: na razie dziekuje Ci Potem to sobie zobacze

Antonni: Teraz popatrzylem dokladnie i Mila brakuje w tresci po B=(3,4) polprostych AC i BD itd . Ale mysle ze to nie wplynelo az tak bardzo na tresc . Przepraszam bardzo . Wybacz noc .

Antonni: Qulka jednak mysle ze ten podpunkt C) bedzie zwiazany z podpunktem B) wiec teraz napiszse swoje rozwiazanie podpunktu b)

	b		d
Skoro		>		to bedziemy mieli takie przedzialy
	a		c

	b
1. (−∞, −		)
	a

wtedy f(x)= −ax−b−cx−d f(x)= −x(a+c)−(b+d) ===============

	b		d
2. <−		, −		)
	a		c

mamy wtedy f(x)= ax+b−cx−d f(x)= x(a−c)+b−d) =================

	d
3. <−		,∞)
	c

Tutaj juz prosto f(x)= ax+b+cx+d f(x)= x(a+c)+(b+d) ====================== Teraz bede myslal nad podpunktem C)

Mila: f(x)=|ax+b|+|cx+d| |ax+b|+|cx+d|=x+1 dla x∊<1,3) Dla x=1 oraz x=3 następuje zmiana wzoru f(x). x=1 miejsce zerowe g(x)=ax+b x=3 miejsce zerowe h(x)=cx+d a*1+b=0⇔b=−a c*3+d=0⇔d=−3c L=|ax−a|+|cx−3c| x≥1 i x<3 ax−a+(−cx+3c)=x+1 ax−cx+(−a+3c)=x+1 x*(a−c)+(−a+3c)=x+1 a−c=1 −a+3c=1 a=2 i b=−2 c=1 i d=−3 f(x)=|2x−2|+|x−3|

Antonni: Dziekuje Mila za odpowiedz. Zaraz zapisze w zeszycie i dopytam jeszcze .

Antonni: WIdze Mila ze robilas to przez porownanie do y=x+1 A mozna to jakos zrobic inaczej wykorzystujac wspolrzedne y_owe punktow A i B

	b
bo −		=1 to a=−b
	a

	d
i −		=3 to d=−3c
	c

Teraz jak wykorzystac y₁=2 i y₂= 4 ? Mozna ?

Antonni:

Mila: Spróbuj, przecież wiesz co masz otrzymać.

Antonni: Poprobuje

Antonni: To zostawie juz na jutro .