Wykres Antonni: Rozwiaz rownanie . |y|+y+|x|+x=0 Pytanie . czy tutaj nalezy rozpatrywac przypadki 1|y|≥0 i |x|≥0 2. |y|≥0 i |x|<0 3. |y|<0 i |x|≥0 4. |y|<0 i |x|<0 Potem zrobic wykres?

marek: zawsze, jeżeli mamy wartość bezwzględną i jeszcze niewiadomą poza wartością, lub dwie niezależne, lub więcej niezależnych wartości bezwzględnych to musimy rozpatrywać przypadki. Wykresu nie trzeba.

marek: no dobra... zawsze poza szczególnymi przypadkami, np. |x−1|+|y−2|=0

Antonni: Dziekuje CI na razie marek

Eta: |x|+|y|= −(x+y) x=0 i y=0

Antonni: Dziekuje CI rowniez . Za chwile napisze rozwiazanie z ksiazki tylko zrobie sobie opatrunek .

piotr: rozwiązaniem jest trzecia ćwiartka wraz z półosiami x≤0 i y≤0

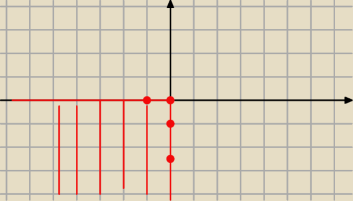
Eta: Racja piotr x≤0 i y≤0

Antonni: Przepraszam ale mam uszkodzona lewa reke i musialem zrobic opatrunek Piszse tak Dla kazdego x∊R |x|+x≥0 i dla kazdego y∊R |y|+y≥0 wiec |y|+y+|x|+x=0 ⇔(|x|+x=0 i |y|+y=0)⇔(x≤0i y≤0) Troche za bardzo tego nie rozumiem dlatego zapytalem o te przypadki

piotr: 1y≥0 i x≥0 ⇒ 2x+2y=0 ⇒ x=0 y=0 2. y≥0 i x<0 ⇒ 2y = 0 ⇒ y=0, x<0 3. y<0 i x≥0 ⇒ 2x=0 ⇒ x=0, y<0 4. y<0 i x<0 ⇒ 0=0 ⇒ y<0 i x<0 ⇒⇒⇒⇒ x≤0 i y≤0

Antonni: Wiec juz dostalem odpowiedz na moje pytanie . dziekuje bardzo