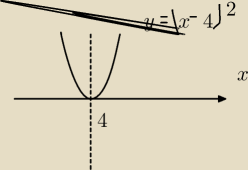
Granica jednostronna, problem... Macko z Bogdanca: Granica jednostronna, problem...

Lim
	U{x2−x−12}{(x−4)2
x→4−

	1
x→4−,to (x−4)2→0+ , wiec		→+∞
	(x−4)2

Lim		x2−x−12		Lim		1
			=		(x2−x−12)(		)
x→4−		(x−4)2		x→4−		(x−4)2

	Lim		1		12		1
=		x2(1−		−		)(		)=+∞
	x→4−		x		x2		(x−4)2

Ma wyjsc −∞. Co robie zle?

Saizou :

x2−x−12		(x−4)(x+3)		x+3
	=		=
(x−4)2		(x−4)2		x−4

pochodzimy z lewej strony, więc można sobie rozumować że czymś minimalnie mniejszym niż 4,

	7
wówczas mianownik jest ujemny a licznik dodatni, jako symbole to będzie [		], czyli −∞
	0−

Qulka: x²−x+12=(x−4)(x+3) skróć

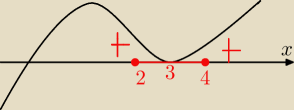
Macko z Bogdanca: W ksiazce mialem jakos tak to tlumaczone na takim przykladzie

lim		2x−7
x→3		(x−3)2(x+2)

2x−7		2x−7
	→0+ wiec		→+∞
(x−3)2(x+2)		(x−3)2(x+2)

lim		2x−7		lim		1
			=		(2x−7)		=−∞
x→3		(x−3)2(x+2)		x→3		(x−3)2(x+2)

Myslalem ze jak u mnie w mianowniku jest parabol ktora nie przecina osi x to po lewej stronie oraz po prawej bediemy mieli

	1
,,+'' wiec		→+∞
	(x−4)2

Macko z Bogdanca: Wiec cos zle interpretuje z ksiazki czy gdzies sie wywalilem ?

Qulka: przy granicach w punkcie nie wyciągasz np x² przed nawias bo powstałe ułamki się nie zerują u Ciebie jak wstawiłbyś 4 to na górze i na dole wychodzi 0/0 więc nieoznaczoność

Macko z Bogdanca: ok, dziekuje