Funkcja wykladnicza Pati18773:

	1
Dla jakich wartości m zbiór wartości funkcji f(x)=(		)(m−2mx−x2) jest zawarty w
	2

przedziale <1;+∞)

Pati18773: Tam ta 1/2 jest do potegi m−2mx−x²

Jack: masz na mysli

	1
(		)m − 2mx − x2 ?
	2

Pati18773: Tak

Jack:

	1
Jest zawarty gdy mamy (		)do potegi ≤ 0
	2

	1
gdyz dla 0 mamy (		)0 = 1, dla − 1 mamy 2 itd
	2

zatem pozostaje rozwiazac nierownosc m − 2mx − x² ≤ 0

Pati18773: Stwierdziłam że m−2mx−x2≤0 Wyliczyłam delte i musi być ona wieksza od 0 ?

Pati18773: No to tak zrobilam

Jack: dobre pytanie...

Jack: ale chyba tak... Δ ≥ 0

Jack: chociaz na razie nie jestem tego taki pewien...

Pati18773: Ramiona wykresy będą do góry czy na dół ?

Pati18773: No ja tak samo

Pati18773: W odpowiedzi jest że m €<−1;0>

Jack: to oni zrobili dla Δ ≤ 0

Pati18773: No tylko nie wiem dlaczego

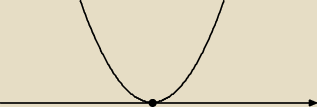
Jack: Przeanalizujmy ten przykład mamy funkcje m − 2mx − x² ≤ 0 /*(−1) x² + 2mx − m ≥ 0 jest to parabola, ramiona skierowane do gory. dla Δ ≤ 0 (patrz rysunek), funkcja ta nie ma rozwiazan (lub ma 1), tj. nie ma miejsc zerowych (lub ma 1) zatem jest ≥ 0 dla kazdej x ∊ R, czyli dowolne m spelnia to rownanie... dla Δ ≥ 0 uzyskamy taki przedzial x, gdzie nie bedzie spelnial rownania... wiec tez m nie bedzie? hmm chyba oto chodzi zeby jednak kazdy x spelnial.

Pati18773: Kurczę teraz to już sama nie wiem może w odpowiedzi jest błąd

Jack: odp. sie zgadza musi byc delta ≤ 0