Wykresy z wartoscia bezwzgledna Antonni: Dane sa liczby d>c>b>a>0 A) Sporzadz wykres funkcji f(x)= |x−d|+|x−c|+|x−b|+|x−a| dla dowolnie obranych licz a,b, c, d B) Podaj najmniejsza wartosc tej funkcji C) Czy jest to jej minimum w sensie definicji 13.10 Piszse tta definicje . Mowimy ze funkcja f(x) osiaga maksimum w punkcie x₀ , wtedy gdy istnieje takie otoczenie U punktu x₀ w ktorym funkcja ta jest okreslona i ∀x∊U (x≠x₀⇒f(x)<f(x₀) ) Podobnie okreslamy minimum funkcji w punkcie x₀ A) Zrobilem wykres tej funkcji Bedzie tak f(x)= −4x+(a+b+c+d) dla x<a f(x)= −2x+(−a+b+c+d) dla a≤x<b f(x)= −a−b+c+d dla b≤x<c f(x)= 2x+(−a−b−c+d) dla c≤x<d f(x)= 4x+(−a−b−c−d) dla d≤x W pozostalych punktach prosze o pomoc

Antonni:

Qulka: dla dowolnie obranych liczb ... oznacza że masz sobie wybrać jakieś konkretne cztery liczby i dopiero wykonać

Antonni: Dobry wieczor . Tak ja to zrobilem w zeszycie Mam tylko odpowiedz w ksiazce bez wytlumaczenia ze B) najmniejsza wartosc tej funkcji to :−a−b+c+d (dlatego rozpisalem na przedzialy tak C) Nie .

Qulka: B) jak zrobiłeś obrazek to widzisz gdzie ma minimum ... C) to minimum to płaska więc nie spełnia nierówności

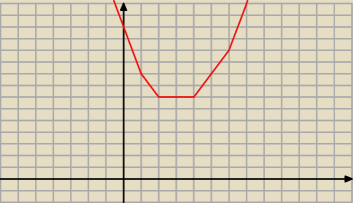
Antonni: Tak zrobilem w zeszcie f(x)= |x−6|+|x−4|+|x−2|+|x−1| Dziekuje CI za odpowiedz . Polecam sie przy nastepnych

Antonni: Moze jednak ktos chcialby to wytlumaczyc ten punkt B) bo to jest zadanie maturalne i pewnie cos wiecej nalezy napisac . dziekuje .

Qulka: porównaj to z tą wartością najmniejszą wstawiając zamiast x a±Δ b±Δ potem c±Δ i d±Δ

Antonni: Dobrze Qulka Wroce do tego juz jutro (moze bedziesz do poludnia na forum ?

Qulka: może się uda

Antonni: Ok

Antonni:

Antonni: Qulka Znalazlem rozwiazanie punktu B w inny zbiorze zadan (nie rozumiem go za bardzo Dowod I x<a<b ⇒−4x>−2a−2b⇒−4x+a+b+c+d>−2a−2b+a+b+c+d=−a−b+c+d II a≤x<b⇒−2x>−2b⇒−2−a+b+c+d>−2b−a+b+c+d=−a−b+c+d III c≤x<d⇒2x>2c⇒2x−a−b−c+d≥2c−a−b−c+d= −a−b+c+d iV d≤x ⇒4x>2c+2d⇒4x−a−b−c−d≥2c+2d−a−b−c−d= −a−b+c+d

Qulka: no to jest to co mówiłam... żeby potraktować x jako a,b,c,d odpowiednio trochę większe i mniejsze i porównać z tym minimum

Antonni: Szkoda ze musialem wyjechac gdy odpisalas Moze bedziesz wieczorem .

Qulka: jeżeli północ nazwiemy wieczorem to na pewno będę

Antonni: Dzien dobry Qulka tak. Moze byc o polnocy , gdyz ja tez zaczynam o tej porze myslec ( troche mi sie te pory (nie spodnie ale dnia przestawily

Qulka: no więc co jest dziwne

Antonni: WItaj Juz pisze Dlaczego np w I wstawaimy −2a−2b a np w III tylko 2c? (chodzi o post 11:34

Antonni: Oczywiscie nie pali sie tak z tym

Qulka: bo chcemy to porównać z tym minimum .. więc tak dobieramy żeby się poskracało

Antonni: Dobrze . dziekuje CI Zapisze to sobie zeszycie w uwagach do zadnka