Dowód istnienia równoległoboku - kąty i trójkąty
Sinus: Mamy dany trójkąt ostrokątny ABC. Odcinki AD, BE to wysokości tego trójkąta.Punkt M dzieli bok
AB na dwie równe części. Punkty P, Q są symetryczne do punktu M względem odpowiednio prostych
AD, BE. Udowodnij, że środek odcinka DE leży na prostej PQ.
Zrobiłem rysunek i mam pomysł jak to zrobic. Mianowicie, możnaby dowieśc, że PQ i DE to
przekątne równoległoboku EQDP, czyli przecinałyby się w połowie. Problem tylko, że nie wiem
jak dowieśc, że EQDP to równoległobok i w tym miejscu stanąłem, nie wiem jak to ugryźc. Czy
operowac na kątach czy może probowac pokazac że przeciwległe boki są równoległe i sobie równe.
Help

28 wrz 20:38
alex:
28 wrz 20:54
Sinus:
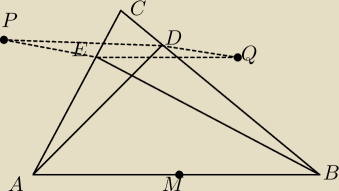
Mniej więcej tak to wygląda. Tu mi tylko wyszedł ten równoległobok strasznie płaski. Ktoś coś
podpowie ?

28 wrz 21:22
Sinus: Hmm AMQE też wygląda na równoległobok... naprawdę nikt nic nie widzi ?

28 wrz 21:57
Sinus: MBDP też mi wygląda na równoległobok... ktoś wie jak to można wykorzystac ? Ludzi odezwijcie
się, bo nwm czy sam tu jestem z tym czy co

28 wrz 22:01
Kacper:

28 wrz 22:18
Qulka: x=AM=BM=BQ=QE=AP=PD
28 wrz 22:32
Sinus: No przecież... ech, w geometrii albo ma się szczęście i coś zauważy albo można się męczyc
godzinami, dziękuję Qulka

28 wrz 23:23
Dan:
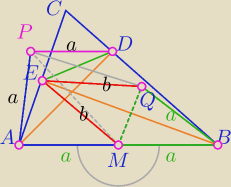
ΔMQB− Δrównoramienny,
Prosta EB− symetralna odcinka MQ
|MB|=|BQ|=a
|EM|=|EQ| =b Każdy punkt symetralnej jest jednakowo odległy od końców odcinka MQ
Podobnie
Prosta AD− symetralna odcinka PM
|AP|=|AM|
|PD|=|MD|
Dlaczego Qulko
EQ=BQ ?
28 wrz 23:33
Qulka: bo MQ dzieli BE powiedzmy w W
ponieważ ΔABE jest podobny do ΔMBW w skali 2 zatem BW =WE
a z podobieństwa bkb ΔBWQ = ΔEWQ
albo z tego że wysokość WQ dzieli na połowy BE gdy równoramienny
28 wrz 23:49
Dan:
Dziękuję.
29 wrz 00:05

 Mniej więcej tak to wygląda. Tu mi tylko wyszedł ten równoległobok strasznie płaski. Ktoś coś
podpowie ?
Mniej więcej tak to wygląda. Tu mi tylko wyszedł ten równoległobok strasznie płaski. Ktoś coś
podpowie ? 




 ΔMQB− Δrównoramienny,
Prosta EB− symetralna odcinka MQ
|MB|=|BQ|=a
|EM|=|EQ| =b Każdy punkt symetralnej jest jednakowo odległy od końców odcinka MQ
Podobnie
Prosta AD− symetralna odcinka PM
|AP|=|AM|
|PD|=|MD|
Dlaczego Qulko
EQ=BQ ?
ΔMQB− Δrównoramienny,
Prosta EB− symetralna odcinka MQ
|MB|=|BQ|=a
|EM|=|EQ| =b Każdy punkt symetralnej jest jednakowo odległy od końców odcinka MQ
Podobnie
Prosta AD− symetralna odcinka PM
|AP|=|AM|
|PD|=|MD|
Dlaczego Qulko
EQ=BQ ?