Nierówność logarytmiczna Elektronik_Radom: Zaznacz w układzie współrzędnych zbiór punktów (x,y) , dla których współrzędne spełniają nierówność logx y < logy x . Mam takie zadanie i umiem je rozwiazac do pewnego momentu przy ktorym staje i nie wiem co robic. Moje rozwiazanie: log_x y < log_x x/ log_x y log_x y < 1/ log_x y (log_x y)² − 1/ log_x y <0 t=log_x y t² − 1/t <0 t(t−1)(t+1)<0 t∊(−∞,−1) U (0,1) no i dalej nie wiem co robic moze ktos pomoc znam odpowiedz ktora brzmi tak: log_x y <−1 v 0< log_x y < 1 y<1/x dla x>1 v 1<y<x dla x>1 y>1/x dla x<1 1>y>x dla x<1 Ale dlaczego tak to nie mam pojecia / POMOCY!

Elektronik_Radom: Umiałby ktoś mi to wytłumaczyć Uczę się do klasówki i paru szczegółów, ważnych szczegółów nie rozumiem

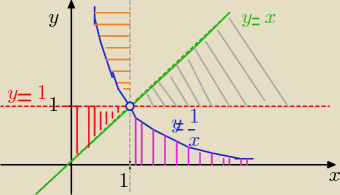Eta: brązowy −−− to y>¹_x dla x€(0,1) fioletowy −−− to dla y <¹_x dla x >1 [szary] −−− to dla 1<y<x dla x >1 czerwony −−− to dla 1>y>x dla x€(0,1) oczywiście punkt ( 1,1) nie należy do tego zbioru i wszystkie punkty na hiperboli i na prostej y = x i na prostej y=1 i na prostej x =1 oraz na osiach OX i OY też nie należą do tego zbioru Po pierwsze: konieczne założenia: x >0 i y>0 i x ≠1 i y≠1 ponad to funkcja log a_x −−− jest rosnąca dla x€(0,1) −−− jest malejąca dla x >1 dlatego też : dla x >1 nierówność zachowuje zwrot log_xy[ < −1 to y< x⁻¹ => y < ¹_x dla x€(0,1) następuje zmiana zwrotu tej nierówności log_xy <−1 to: y >¹_x podobnie i w drugim przypadku: dla x >1 0< log_x y<1 => 1< y< x a dla x€ ( 0,1) 0<log_xy<1 => 1> y >x teraz zaznacz te punkty ( x, y) w układzie współrzędnych pamietając o przedziałach dla "x"