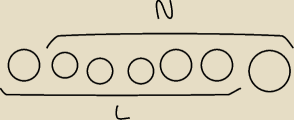
Co jest nieprawidłowe w poniższym założeniu indukcyjnym i dowodzie? Emilia: Co jest nieprawidłowe w poniższym założeniu indukcyjnym i dowodzie? Odpowiedź podobno jest bardzo prosta. Dołączam rysunek pomocniczy. Kółka reprezentują dzieci. Założenie: Wszystkie dzieci mają ten sam kolor oczu Dowód: Załóżmy że mamy n dzieci. Twierdzenie jest oczywiste dla n=1. Załóżmy iż założenie jest prawdziwe dla n=k dzieci. Bierzemy pod uwagę k+1 dzieci. Możemy założyć za pomocą indukcji że w zbiorze L zawierającym k dzieci, wszystkie dzieci mają ten sam kolor oczu. Tak samo możemy założyć że wszystkie k dzieci w zbirze R ma również ten sam kolor oczu. Wtedy jest oczywiste że k+1 dzieci ma ten sam kolor oczu, ponieważ dziecko całkowicie z lewej strony i dziecko całkowicie z prawej strony ma ten sam kolor oczu co dzieci pomiędzy. W taki sposób udowodniliśmy przy pomocy indukcji że w zbiorze zawierający n dzieci wszystkie mają ten sam kolor oczu, niezależnie od tego jaką n ma wartość. Dlatego też wszystkie dzieci mają ten sam kolor oczu.

jc: Nie przejdziesz w ten sposób z n=1 do n=2.

Emilia: Dlaczego?

PW: Już pierwszy krok indukcyjny jest błędny. Stwierdzenie "jedno dziecko ma ten sam kolor oczu" jest tyleż prawdziwe, co nieadekwatne do postawionej tezy. Należało zacząć od n = 2, a wtedy sprawdzenie (pierwszy krok indukcyjny) nie daje zdania prawdziwego (w sensie "nie jest zawsze prawdziwe").

PW: Jeszcze powiem to w inny sposób: Zdanie "Wszystkie dzieci mają ten sam kolor oczu" należy rozumieć jako "Każda dowolnie wybrana dwójka dzieci ma ten sam kolor oczu", a więc sprawdzanie dla n=1 nie jest sensowne, pierwsze sprawdzenie powinno być dla n = 2.