 eh, pewnie istnieje krotszy sposob, no ale nie przychodzi mi na mysl poki co.
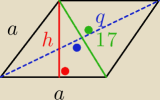
Niech p i q beda przekatnymi, h − wysokoscia, a − bokiem rombu, P − pole rombu.
h = 8
p = 17
P = ah = 8a
eh, pewnie istnieje krotszy sposob, no ale nie przychodzi mi na mysl poki co.
Niech p i q beda przekatnymi, h − wysokoscia, a − bokiem rombu, P − pole rombu.
h = 8
p = 17
P = ah = 8a
| 1 | ||
P = | * 17 * q | |
| 2 |
| q | 17 | |||
( | )2 + ( | )2 = a2 | ||
| 2 | 2 |
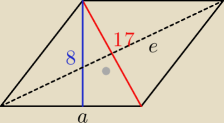 P1=P2
P1=P2
| 1 | ||
ah= | ef | |
| 2 |
| 1 | ||
a·8= | ·17·e | |
| 2 |
| 17 | ||
a= | e | |
| 16 |
| 17 | e | 17 | ||||
( | )2+( | )2=( | e)2 | |||
| 2 | 2 | 16 |
| 289 | e2 | 289 | |||
+ | = | e2 | |||
| 4 | 4 | 256 |
| 18496 | ||
e2= | ||
| 225 |
| 136 | ||
e= | ||
| 15 |
| 17 | 136 | 1156 | ||||
P=8· | · | = | ||||
| 16 | 15 | 15 |

 . Ten romb był wpisany w czworokąt w taki sposób,
że wierzchołki rombu są w połowie boków czworokąta. W odpowiedzi było pole tego
czworokąta − a ono jak wiadomo jest 2 razy większe od pola tego rombu. Dzięki wielkie
. Ten romb był wpisany w czworokąt w taki sposób,
że wierzchołki rombu są w połowie boków czworokąta. W odpowiedzi było pole tego
czworokąta − a ono jak wiadomo jest 2 razy większe od pola tego rombu. Dzięki wielkie 
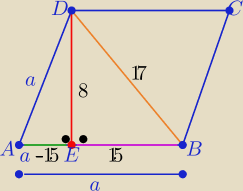 Inny sposób
Z tw. Pitagorasa w ΔEBD : |EB|= P{172−82}= 15
to |AE|= a−15 , a∊(0,15)
ponownie z tw. Pitagorasa w ΔAED :
Inny sposób
Z tw. Pitagorasa w ΔEBD : |EB|= P{172−82}= 15
to |AE|= a−15 , a∊(0,15)
ponownie z tw. Pitagorasa w ΔAED :
| 17*17 | ||
64+(a−15)2=a2 ⇒ a= | ||
| 30 |
| 1156 | ||
P=a*h=........ = | [cm2] | |
| 15 |