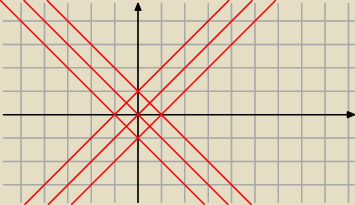
Wykres stinger: Przedstaw graficznie równanie |x|+x²=|y|+y²

Saizou : |x|−|y|=y²−x²=(y−x)(y+x) dla x≥0 i y≥0 mamy x−y=−(x−y)(y+x) + zał x≠y 1=−(y+x) dla x=y równość jest prawdziwa y=−x−1 dla x≥0 i y<0 mamy x−(−y)=(y−x)(y+x) x+y=(y−x)(y+x) +zał x≠−y, dla −x=y równosć prawdziwa 1=y−x y=−x+1 dla x<0 i y≥0 mamy −x−y=(y−x)(y+x) + zał y≠−x, gdy x=−y równość prawdziwa −1=y−x y=x−1 dla x<0 i y <0 −x+y=(y−x)(y+x) +zał y≠x 1=y+x y=x−1

PW: Coś Ci tym razem wyjątkowo nie wierzę. Przecież jeżeli |x| > |y|, to x² > y² i po dodaniu stronami |x| + x² > |y| + y², a więc nie ma równości. Podobnie przy odwrotnej relacji między modułami x i y. Równość jest możliwa tylko wtedy, gdy |x| = |y|.

Kacper: Tylko proste y=x i y=−x

Saizou : owszem, moja wina