Parzystosc i nieparzystosc Antonni: Funkcje f₁ i f₂ sa parzyste funkcje g₁ i g−2 sa nieparzyste Wszystkie one okreslone sa w tej samej dziedzinie D Zbior wartosci tych tych funkcji jest podzbiorem D Zbadaj parzystosc nastepujacych funkcji a) f₁+f₂ b) g₁+g₂ c) f₁+g₁ d) f₁*f₂ e) g₁*g₂ f) f₁*g₁ g) zlozenie g₂ z g−1 , h) zlozenie f₂ z f₁ i) zlozenie g₁ z f₁ To jest dla mnie trudne Funkcja parzysta f(x)= f(−x) nieparzysta f(x)= −f(x) to wiem

Antonni:

Antonni: Ma byc g₂ a nie g−2

Antonni: tak samo g₁ a nie g−1

Antonni: Dla mnie to zadanie jest trudne ale czy wszystkich tutaj to zadanie przerasta ze nikt nie potrafi od godziny pomoc ?

ICSP: f₁ parzysta ∀_{x ∊ D} f₁(x) = f₁(−x) analogicznie dla f₂ a) Oznaczmy: h(x) = f₁(x) + f₂(x) Wtedy ∀_{x \in D} mamy h(x) = f₁(x) + f₂(x) = f₁(−x) + f₂(−x) = h(−x) Co oznacza, że h jest funkcją parzystą. Pozostałe przykłady robi się analogicznie. Jeśli coś nie wychodzi to postaraj się szukać kontrprzykładów.

Antonni: Dziekuje Ci ICSP A moglbys pokazac te zlozenia bo tego to juz nie rozumiem ?

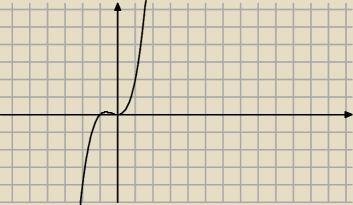
Antonni: Bo np zrobilem wykres funkcji y=x²+x³ gdzie y=x² to funkcja parzysta i y= x³ to funkcja nieparzysta Wychodzi na to z suma tych funkcji to funkcja ani parzysta ani nieparzysta Najbardziej to chodzi o te zapisy

ICSP: f₁ = x² , g₁ = x³ Oznaczmy : h(x) = x³ + x² h(−x) = −x³ + x² ≠ x³ + x² = h(x) − h nie jest parzysta h(−x) = −x³ + x² ≠ −(x³ + x²) = −h(x) − h nie jest nieparzysta.

ICSP: g₁ , g₂ − nieparzyste h(x) = g₁(g₂)(x) = (g₁ ◯ g₂)(x) h(−x) = (g₁ ◯ g₂)(−x) = g₁(g₂(−x)) = g₁(−g₂(x)) = −g₁(g₂(x)) = −(g₁ ◯ g₂)(x) = −h(x) h jest nieparzysta.

Antonni: Bardzo Ci dziekuje

Antonni: To sa zadania maturalne z troche starszego zbioru zadan ale chcialem sie z nimi zapoznac .