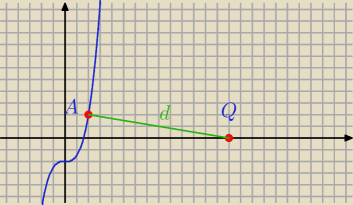
 Q = ( 14, 0)
A = ( x, 0,5 x3 − 2)
→
QA = [ x − 14, 0,5 x3 − 2]
d = √(x − 14)2 + ( 0,5 x3 − 2)2 =√x2 − 28 x + 196 + 0,25 x6 − 2 x3 + 4 =
= √0,25 x6 −2 x3 + x2 −28 x + 200
g(x) = 0,25 x6 − 2 x3 + x2 − 28 x + 200
g '(x) = 1,5 x5 − 6 x2 + 2 x − 28 = 0 ⇔ x = 2
g ''(x) = 7,5 x4 − 12 x + 2
g ''(2) > 0 więc funkcja g osiąga minimum dla x = 2.
A = (2 , 2)
→
QA = [ 2 − 14, 2 − 0] = [ − 12, 2]
d = √144 + 4 = √148 = 2√37
Q = ( 14, 0)
A = ( x, 0,5 x3 − 2)
→
QA = [ x − 14, 0,5 x3 − 2]
d = √(x − 14)2 + ( 0,5 x3 − 2)2 =√x2 − 28 x + 196 + 0,25 x6 − 2 x3 + 4 =
= √0,25 x6 −2 x3 + x2 −28 x + 200
g(x) = 0,25 x6 − 2 x3 + x2 − 28 x + 200
g '(x) = 1,5 x5 − 6 x2 + 2 x − 28 = 0 ⇔ x = 2
g ''(x) = 7,5 x4 − 12 x + 2
g ''(2) > 0 więc funkcja g osiąga minimum dla x = 2.
A = (2 , 2)
→
QA = [ 2 − 14, 2 − 0] = [ − 12, 2]
d = √144 + 4 = √148 = 2√37
| d | |
d2(x) = 2(x−14) + 2(12x3−2)*32x2 = 32x5 − 6x2 + 2x − 28 | |
| dx |
