Największa wartość funkcji Qwadrat: Największa wartość funkcji

	1
f(x) =		w przedziale <−3, −2> jest równa:
	√x2−1

	√3		√2
A.1 B.		C.2√2 D,
	3		4

Obliczyłem, że:

	√2
f(−3) =
	4

	√3
f(−2) =		− to jest największa wartość funkcji, więc poprawna odpowiedź to B
	3

Chciałbym jednak wiedzieć czy −3 i −2 to jedyne elementy, dla których powinienem sprawdzić wartość, czy może coś jeszcze powinienem wziąć tu pod uwagę (tak jak to ma miejsce przy funkcji kwadratowej, gdzie sprawdza się jeszcze wierzchołek)

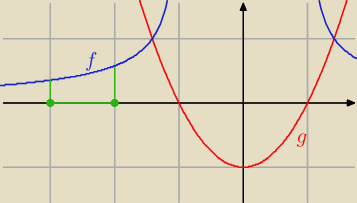
Janek191: Największa wartość funkcji f będzie wtedy, gdy funkcja g(x) = x² − 1 będzie miała najmniejszą wartość

PW: Samo podstawienie krańców przedziału nic nie daje. Na pierwszy rzut oka nic nie wiadomo o funkcji f na tym przedziale (jest rosnąca, czy malejąca, czy może ma ekstremum wewnątrz przedziału). Trzeba zacząć od zbadania jakie wartości przyjmuje x¹ − 1, potem jakie wartości przyjmuje √x² − 1, i na koniec jakie f(x).

PW: Janku, nie zdążyłem, moja podpowiedź nie jest komentarzem do Twojej

Janek191: Oczywiście rozpatrujemy te funkcje: f i g w < − 3, − 2>

Qwadrat: Ok, sądzę że rozumiem ogólnie o co chodzi, ale w jaki sposób powinienem zapisać to 'zbadanie'?

PW: Dla x∊,−3, −2> prawdziwa jest nierówność (1) 3 ≤ x² − 1 ≤ 8, gdyż funkcja g(x) = x² − 1 jest na tym przedziale malejąca − największą wartość osiąga dla x = −3, a najmniejszą dla x = −2. Jest to znany fakt, można to stwierdzenie zilustrować wykresem funkcji kwadratowej obciętej do przedziału <−3, −2>. Wobec tego (2) √3 ≤ √x² − 1 ≤ √8 (funkcja "pierwiastek" jest rosnąca, a więc z (1) wynika (2)). Wniosek:

	1		1		1
		≥		≥		,
	√3		√x2 − 1		√8

co oznacza że największą wartością funkcji f jest

	1		√3
		=
	√3		3

(przy okazji widzimy też najmniejszą wartość funkcji f).

Qwadrat: Bardzo dziękuję