całki
Mała Mi: Oblicz pole obszaru ograniczonego krzywą o równaniu y=x2+3x−2 i prostą y=2
23 wrz 10:01
23 wrz 10:04
Jerzy:
Zacznij od ustalenia granic całkowania.
23 wrz 10:05
Jack:
x
2 + 3x − 2 = 2
x
2 + 3x − 4 =0
(x+4)(x−1) = 0
1
| | x3 | | x2 | |
∫ (−x2−3x+4)dx = [− |
| − 3 |
| +4x]1−4 = |
| | 3 | | 2 | |
− 4
| | 1 | | 3 | | 64 | |
= − |
| − |
| + 4 − ( |
| − 24 −16)= |
| | 3 | | 2 | | 3 | |
| | 13 | | 56 | | 13 | | 112 | | 125 | |
= |
| − (− |
| ) = |
| + |
| = |
| |
| | 6 | | 3 | | 6 | | 6 | | 6 | |
23 wrz 10:18
Puma: Jack
O tej godzinie i z calek to tylko egzamin poporawkowy
Przeciez wiedziales

23 wrz 10:23
Mała Mi: Egzamin dopiero popołudniu!

Ale dziękuję za pomoc!
23 wrz 10:33
Jack: 
Ja calek nie umiem wiec jest szansa ze to jest zle

23 wrz 10:47
Janek191:
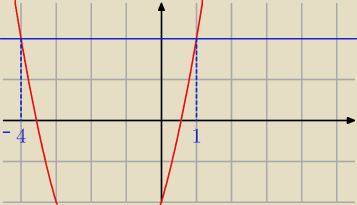
24 wrz 08:32
zef:
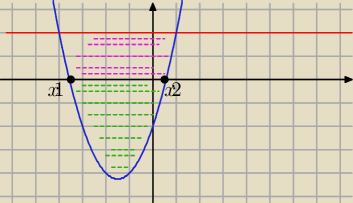
Sprawdził ktoś to rozwiązanie?
czy nie trzeba dzielić tego na 2 przedziału ze względu na to że część jest pod osią Y ?
−∫
x1x2x
2+3x−2dx+∫
−41x
2+3x−4dx
czy liczy się to po prostu:
−∫
−41x
2+3x−4dx
Wypowie się ktoś bo zastanawia mnie to jak się to liczy kiedy część obszaru jest nad osią x a
część pod
24 wrz 11:08
yht:
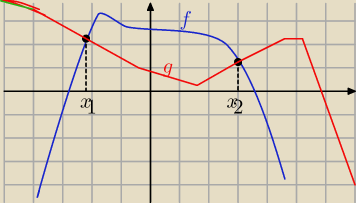
zef, nie trzeba dzielić ze względu na to że część jest pod osią
ogólnie, pole między wykresami f(x) i g(x) liczy się z takiego schematu:
∫
x1x2 f(x) − g(x) dx
24 wrz 11:19
zef: A co jeśli cały obszar jest pod osią ? Pamiętam miałem taki przypadek że musiałem postawić
minus przed całką aby ten obszar nie był ujemny. Kiedy ten minus jest potrzebny przed całką ?
24 wrz 11:21
yht:
być może od dolnego ograniczenia (czyli g(x)) odjąłeś górne (czyli f(x)), stąd musiałeś mieć
minusa przed całką żeby pole było ujemne
albo np. zamieniłeś miejscami granice całkowania
24 wrz 14:02
yht:
*żeby pole nie było ujemne
24 wrz 14:03
zef: Racja, najprawdopodobniej odjąłem dolną funkcję od górnej, masz rację, dzięki

24 wrz 15:39

 Ale dziękuję za pomoc!
Ale dziękuję za pomoc!
 Ja calek nie umiem wiec jest szansa ze to jest zle
Ja calek nie umiem wiec jest szansa ze to jest zle 

 Sprawdził ktoś to rozwiązanie?
czy nie trzeba dzielić tego na 2 przedziału ze względu na to że część jest pod osią Y ?
−∫x1x2x2+3x−2dx+∫−41x2+3x−4dx
czy liczy się to po prostu:
−∫−41x2+3x−4dx
Wypowie się ktoś bo zastanawia mnie to jak się to liczy kiedy część obszaru jest nad osią x a
część pod
Sprawdził ktoś to rozwiązanie?
czy nie trzeba dzielić tego na 2 przedziału ze względu na to że część jest pod osią Y ?
−∫x1x2x2+3x−2dx+∫−41x2+3x−4dx
czy liczy się to po prostu:
−∫−41x2+3x−4dx
Wypowie się ktoś bo zastanawia mnie to jak się to liczy kiedy część obszaru jest nad osią x a
część pod
 zef, nie trzeba dzielić ze względu na to że część jest pod osią
ogólnie, pole między wykresami f(x) i g(x) liczy się z takiego schematu:
∫x1x2 f(x) − g(x) dx
zef, nie trzeba dzielić ze względu na to że część jest pod osią
ogólnie, pole między wykresami f(x) i g(x) liczy się z takiego schematu:
∫x1x2 f(x) − g(x) dx
