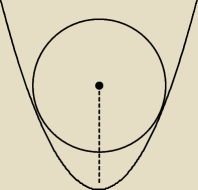
Dowód, parabola, pochodne Emilia: y=x² Udowodnij że odległość od środka okręgu to dna paraboli = r²+1/4 Trzeba chyba wykorzystać w jakiś sposób pochodne, nie mam jednak pomysłu jak to udowodnić? Proszę o pomoc.

Jerzy: A co wiadomo o tym okręgu ?

Emilia: tyle ze ma promien r

Jack: czyli nie wiemy gdzie jest srodek okregu?

jc: Punkty na paraboli: (x,x²). Wektor styczny: (1,2x). Wektor do niego prostopadły: (2x, −1). Od punktu (x,x²) idziemy do osi oy w kierunku wektora (2x,−1): x+2xt = 0, x²−t = y (pionowa współrzędna środka okręgu) t = −1/2 y = x²+1/2. r² = t² (4x²+1) = x² + 1/4 (kwadrat przebytej drogi) y = r² + 1/4

jc: Jack, wiemy gdzie jest środek okręgu. Oczywiście, czym większy okrąg, tym wyżej leży jego środek. Treścią zadania jest znalezienie środka.

piotr1973: równanie prostej prostopadłej do paraboli w x₀ z podstawieniem: x = 0 i y= y₀ (y₀ współrzędna środka okręgu) y₀ = x₀²−(0−x₀)/(2 x₀) równanie odległości (0,y₀) od (x₀, x₀²) x₀²+(y₀−x₀²)² = r² ⇒x₀ = 1/2 √4 r²−1, y₀ = 1/4 (4 r²+1)

Leszek: Koledzy zrobiliscie bledy,przeciez odleglosc nie moze zawierac r²,gdyz byloby w cm²

jc: Leszek, rozwiąż zadanie przyjmując y = x²/a. Problem zniknie.

piotr1973: Leszek, a co np. oznacza wartość x²? czy to jest pole czy odległość danego punktu od osi OX

Leszek: Odleglosc y=x² jest nadal odlegloscia P(x,y) Odleglosc punktu A(x,y) od punktu B(x1,y1) okreslona jest wzorem d= √(x−x1)² +(y−y1)²) Czyli okreslona jest np w centymetrach a nie w cm²

piotr1973: wzór: y₀ = 1/4 (4 r2+1) określa, że odległość y₀ zależy od promienia w kwadracie i tyle y₀ jest funkcją zmiennej r y₀(r) = 1/4 (4 r2+1)