Konstrukcja
Twoja Droga:
Dzień dobry
Dany jest okrąg o(O,R) prosta L nie mająca z danym okręgiem punktu wspólnego oraz punkt A
należący do prostej L. Zbudować okrąg styczny do danego okręgu oraz do prostej L w punkcie A.
Pozwoliłam sobie zaznaczyć szukany okrąg jako o(Q,r), gdzie |OA| jest prostopadłe do prostej L
w tym przypadku Q=1/2A+1/2P, punkt P należy do obydwóch okręgów czyli jest punktem styczności
tych że okręgów . . . Teraz potrzebuje pomocy w rozważeniu 2 przypadku przedstawionego na
rysunku. Potrzebuje jednej konkretnej pomocy jak wyznaczyć ten mniejszy okrąg o(Q,r) gdy jest
dany tylko ten duzy i A∊L ?
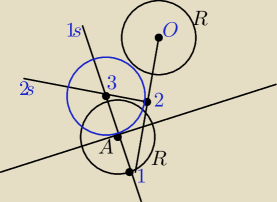1.wyznaczam prostopadłą s1
2. wyznaczam punkt 1 jako przecięcie prostopadłej s1 i okręgu o promieniu R i środku w A
3.łączę punkt 1 z punktem O
4. symetralna powstałego odcinka przecina prostopadłą s1 w punkcie 3. który jest środkiem
szukanego okręgu