Pilne delka: 1. Obrazem punktu P(4,−8) w jednokładności o środku S(−3,−2) jest punkt P1 (−5 1/3,0). Zatem skala tej jednokładności jest równa: Odp. −1/3 2. Pole czworokąta ABCD,gdzie A(−5,−2), B(4,1), C(−2,8), D(−6,3), jest równe: Odp. 53

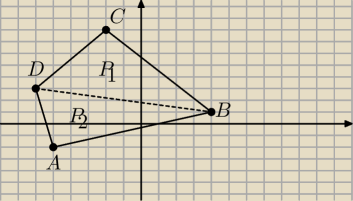
grthx: Obliczyc pole P₁ trojkata DCb Obliczyc pole P−2 trojta DAB DOdac do siebie

Jack: 1. wektor OP ' = k * wektor OP gdzie k to skala, O to srodek jednokladnosci, P to punkt ktory tam wybieramy. zatem [−5¹₃ +3 , 0 + 2] = k * [4 + 3, −8+2] stąd mamy 2 rownania, z ktorych kazde jest rozwiazaniem tego samego k

	1
−5		+ 3 = 7k −>>> k = ...
	3

albo 2 = −6k −>> k = skoro to jest to samo "k" no to latwiej rozwiazac te drugie rownanie zatem

	−2		1
2 = − 6k −>>> k =		= −
	6		3

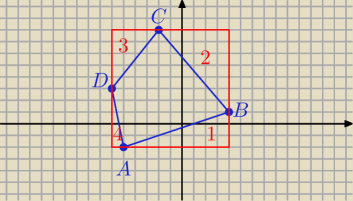
Janek191: Pole czworokąta P = ( 4 − (−6 ))*(8 − (−2)) − 0,5*( 9*3 + 7*6 + 4*5 + 5*1) = 100 − 0,5*(27 + 42 + 20 + 5) = = 100 − 0,5*94 = 100 − 47 = 53 ======================