Proszę o pomoc delka: 1. Obrazem prostej k:2x−y−3=0 w jednokładności o środku O(0,0) i skali k: − 0,75 jest prosta o równaniu : Odp. 8x−4y+9=0 2. Promień okręgu o równaniu x²+y²−2ax−4by+2ab+3b²=0, gdzie a≠b, ma długość: Odp. I b−a I 3. Punkt K jest środkiem ciężkości trójkąta ABC, gdzie A(1,−9), B(7,6), C(−2,12). Zatem wektor CK ma współrzędne: Odp.[4,−9]

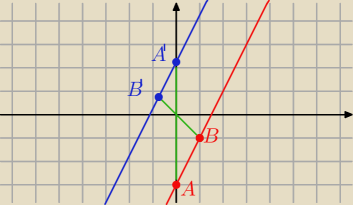
Janek191: k: 2x − y − 3 = 0 y = 2 x − 3 A = ( 0, − 3) B = ( 1, − 1) O = ( 0, 0) k = − 0,75 → → OA ' = − 0,75 OA = − 0,75*[ 0, − 3] = [ 0, 2,25] ⇒ y ' = 2,25 x' = 0 A ' = ( 0, 2,25) Prosta A ' B' y = a x + b a = 2 y = 2 x + b 2,25 = 2*0 + b ⇒ b = 2,25 y = 2 x + 2,25 ==========

Janek191: y = 2 x + 2,25 / * 4 4 y = 8 x + 9 8 x − 4 y + 9 = 0 ===========

Janek191: z.2 x² + y² − 2a x − 4 b y +2a b + 3 b² = 0 ( x − a)² − a² + ( y − 2 b)² − 4 b² +2 a b +3 b² = 0 ( x − a)² + ( y − 2 b)² = a² −2 a b + b² = ( a − b )² ⇒ r = I a − b I

Janek191:

	1 + 7 − 2
xk =		= 2
	3

	− 9 + 6 + 12
yk =		= 3
	3

K = ( 2, 3) C = ( −2 12) więc → CK = [ 2 − (−2), 3 −12 ] = [ 4, − 9 ] ========================

Janek191: C = ( − 2 , 12)

Janek191: A gdzie Delka ?

Mila: Zadanie1. k: 2x−y−3=0 II sposób wsp. punktów po przekształceniu

	3
x'=−		x
	4

	3
y'=−		y
	4

podstawiamy do równania prostej

	4
x=−		x'
	3

	4
y=−		y'
	3

	4		4
2*(−		x')−(−		y')−3=0
	3		3

	8		4
−		x'+		y'−3=0 /*(−3)
	3		3

8x'−4y'+9=0 opuszczamy znaczki 8x−4y+9=0