
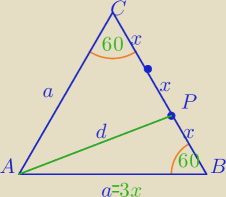
 w ΔABP: x>0
d2=(3x)2+x2−2*3x*x*cos 60o
d2=9x2+x2−3x2
d2=7x2
w ΔABP: x>0
d2=(3x)2+x2−2*3x*x*cos 60o
d2=9x2+x2−3x2
d2=7x2
| d2 | ||
x2= | ||
| 7 |
| d | ||
x= | ||
| √7 |
| 3d | ||
a= | ||
| √7 |
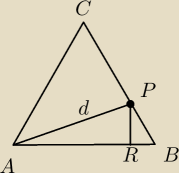 jeśli bok trójkąta to a
możemy wyrazić, |RB|, |RP|, |AB| przez a
z tw. Pitagorasa dostajemy zależność pomiędzy a i d
jeśli bok trójkąta to a
możemy wyrazić, |RB|, |RP|, |AB| przez a
z tw. Pitagorasa dostajemy zależność pomiędzy a i d
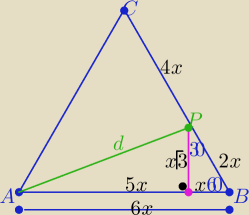
| (6x)2√3 | ||
P(ABC)= | = 9x2√3 | |
| 4 |
| d | d2 | |||
d= √(5x)2+(√3x)2= √28x⇒ d= 2√7x ⇒ x= | to x2= | |||
| 2√7 | 28 |
| d2√3 | 9d2√3 | |||
P=9* | = | |||
| 4*7 | 28 |