Planimetria, związki miarowe w dowolnym trójkącie
Weronika7: W trójkącie o bokach 10,15,20 poprowadzono dwusieczną kąta przeciwległego najdłuższemu bokowi.
Oblicz długość odcinka, który jest częścią wspólną tej dwusiecznej i trójkąta.
20 wrz 22:42
marek: Ta dwusieczna podzieli przeciwległy bok w stosunku 10 do 15.
Teraz np. można użyc dwa razy twierdzenia cosinusów.
20 wrz 23:12
myszka:
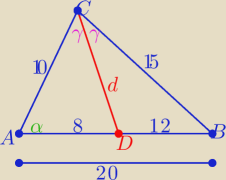
Z twierdzenia o dwusiecznej
| |AD| | | 10 | | 2 | |
| = |
| = |
| to |AD|= 8 i |DB|=12 |
| |DB| | | 15 | | 3 | |
Z tw. kosinusów w ΔABC:
| | 102+202−152 | | 11 | |
cosα= |
| = ... = |
| |
| | 2*10*20 | | 16 | |
i ponownie z tw. kosinusów w trójkącie DAC
| | 11 | |
d2= 82+102−2*8*10* |
| = ... =54 to d= √54= 3√6 |
| | 16 | |
d=3√6
20 wrz 23:46
myszka:
Mila 
20 wrz 23:57
Mila:
21 wrz 00:09