dziwne zadanie
Werkaa: Nie wiem jak zacząć zadanie
Okrąg przechodzi przez punkty A(0,2),B (0,8) i C (8,8).
Następnie środek obwodu i wartość promienia są odpowiednio:
a) (0,5) i 6
b) (5,4) i 5
c) (4,8) oraz 5,5
d) (4,5) i 5
e) (4,6) i 5
19 wrz 23:57
Werkaa: Ktoś? coś?
20 wrz 00:00
Witek: serio dziwne, ma ktoś pomysł?
20 wrz 00:02
Jack:
równanie okręgu to (x−a)2 + (y−b)2 = r2
zatem mozesz podstawiac po kolei te 3 punkty
i otrzymasz uklad 3 rownan z 3 niewiadomymi.
(0−a)2 + (2−b)2 = r2
(0−a)2 + (8−b)2 = r2
(8−a)2 + (8−b)2 = r2
gdzie S(a,b) <−−srodek okregu, r − promien
20 wrz 00:04
Iryt:
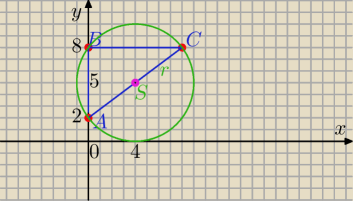
Chyba środek
okręgu ?
A(0,2),B (0,8) i C (8,8).
ΔABC jest trójkątem prostokątnym.
Srodek okręgu opisanego to środek przeciwprostokątnej AC
| | 0+8 | | 2+8 | |
S=( |
| , |
| )= (4,5) co widać, gdy zrobisz rysunek |
| | 2 | | 2 | |
|AC|
2=6
2+8
2
|AC|=10
r=5
20 wrz 00:06
Jack: najszybciej ten uklad rozwiazac (chyba) mozna w ten sposob
Odejmujemy pierwsze 2 rownania.
(2−b)2 − (8−b)2 = 0 (tutaj ze wzoru x2−y2 = (x−y)(x+y)
(2−b−8+b)(2−b+8−b) = 0
10(10−2b) = 0
10 − 2b = 0
b = 5
Teraz idac dalej
odejmuje drugie i trzecie rownanie ze soba
(0−a)2 − (8−a)2 = 0
(−a − 8 +a)(−a + 8−a) = 0
−8(−2a+8) = 0
−2a+8 = 0
a = 4
zatem mamy srodek S(4,5)
podstawiamy do ktoregokolwiek z rownan i liczymy r2 a nastepnie r
a tak wlasciwie to juz widac poprawna odp...
20 wrz 00:09
myszka:
20 wrz 00:10
Witek: DZIĘKUJĘ
20 wrz 00:16
Werkaa: ja bardzo dziękuję
20 wrz 00:16
Iryt:
Maturzyści geometria to rysunek i wszystko widać, to test wyboru, 2 minuty i jest rozwiązanie.
20 wrz 00:24