Geometria martinoo: Proszę o pomoc bo naprawdę nie mam pojęcia jak to zrobić. 1. W trójkącie ABC poprowadzono środkową AD, a następnie narysowano prostą k przechodzącą przez punkt C i przecinającą środkową AD w połowie długości. Oblicz, w jakim stosunku prosta k podzieliła bok AB. 2.Na bokach AC i BC trójkąta ABC obrano punkty P i R. Niech S będzie punktem przecięcia odcinków AR i BP. Oblicz w jakim stosunku dzieli on każdy z tych odcinków, jeśli AP : PC= 3:2, BR:RC=1:5.

Jack: ref?

===: Podstawa to rysunek ... więc rysuj

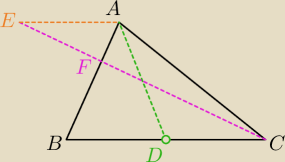
===: zauważ podobieństwo ΔBCF i ΔAEF

	|BC|		|BF|
Skoro		=2 to		=
	|AE|		|AF|

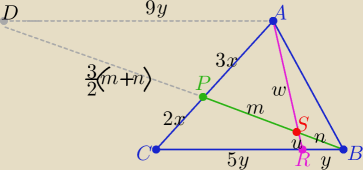
myszka: zad 2/ Z podobieństwa trójkątów ΔDPA ∼ ΔCPB z cechy (kkk)

	|DA|		|AP|		3		3
w skali :		=		=		⇒ |DA|=		*6y = 9y
	|CB|		|PC|		2		2

	3
i |DP|=		(m+n)
	2

oraz z podobieństwa trójkątów ΔBRS ∼ ΔDSA z cechy (kkk)

	9y
w skali		= 9
	y

	w
zatem		= 9 to |AS|: |SR|= 9:1
	u

	|DS|
i		= 9 ⇒ |DS|= 9n
	|SB|

	3		3		5		3
i |DS|=|DP|+|PS| =		m+		n+m=		m+		n
	2		2		2		2

	5		3		n		1
to		m+		n = 9n ⇒ 5m+3n= 18n ⇒ 15n= 5m ⇒		=
	2		2		m		3

zatem: |BS| : |SP|= 1:3

martinoo: Dzięki wielkie ^^

Saizou : Cześć Eto

myszka: Cześć