funkcja Maturzysta: Dana jest funkcja f(x) = log₂(x² − 1) − log₂(1 − x) a) wyznacz dziedzinę funkcji f(IxI) i naszkicuj jej wykres. funkcję uprościłem do takiej postaci: f(x) = log₂(−x − 1) dalej nie mam pojęcia jak to liczyć:(

x: f(|x|)=log₂(x²−1)−log₂(1−|x|) D: x²−1>0 i 1−|x|>0⇔ (x<−1 lub x>1) i |x|<1⇔ (x<−1 lub x>1) i −1<x<1 Brak części wspólnej D=∅ Dobrze przepisałeś?

Maturzysta: tak, dobrze

x: f(x)=log₂(x²−1)−log₂(1−x) D: x²−1>0 i 1−x>0⇔ (x<−1 lub x>1) i 1>x D=(−∞,−1)

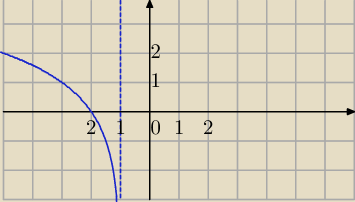
x: f(x)=log₂(−x−1) dla x<−1

Maturzysta: hmm ale ta dziedzina miała być dla funkcji f(IxI)

zef: D∊∅ jeżeli poprzedniej przekształcenia się zgadzają

Maturzysta: i jest jeszcze podpunkt b) rozwiąż nierówność f(IxI) <0

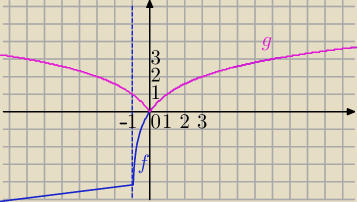
Iryt: y=log₂(x+1) Funkcja f(|x|) Nakładanie wartości bezwzględnej na x. Na wykresie aby powstała funkcja f( |x| ) odbijamy wykres funkcji f(x) leżący po prawej stronie osi OY symetrycznie na lewą stronę OY. Wzór funkcji f(x) zmieniamy na wzór f ( |x| ) Wykres Twojej funkcji leży po lewej stronie OY. zatem nie masz co odbić. Gdybyś miał wzór : f(x)=log₂(x+1) to wykres g(x)=f(|x|) wyglądałby tak jak różowy .

Iryt: Dolna krecha to wada opcji rysuj.