Granica Macko z Bogdanca: Granica lim

	√x+1−√2x+5
x→∞
	x

lim

	(√x+1−√2x+5) (√x+1+√2x+5)
x→∞
	x(√x+1+√2x+5)

lim

	x+1−2x−5
x→∞
	x(√x+1+√2x+5)

lim

	−x−4
x→∞
	x(√x+1+√2x+5)

lim

	x(−1−4x)
x→∞
	x(√x+1+√2x+5)

lim

	−1		−1
x→∞		=		=0
	(√x+1+√2x+5)		∞

W odopowiedziach ma byc 0 i zastanawiam sie czy moge to tak zostawic

Janek191:

	x + 1 − ( 2 x + 5)
f(x) =		=
	x*( √x + 1 + √2x + 5)

	− x − 4
=		=
	x*( √x + 1 + √2 x + 5)

	−1 − 4x
=
	√x + 1 + √2 x + 5

więc

	− 1
lim f(x) =		= 0
	+∞

x→∞

jc: Po co tak kombinować? co to jest ∞ mianowniku −1/∞ ? x ≥ 1 0 ≤ √x+1 / x ≤ √2x / x = √2 / x →0 Podobnie z drugim składnikiem.

grthx: Mozesz bo stala przez nieskonczonosc to 0

Janek191: Stosujemy wzór

	a2 − b2
a − b =
	a + b

Jack: dobrz jest ;x

jc: Co to znaczy stała przez nieskończoność? Janek191, spróbuj znaleźć taką granicę:

	3√x+5 + 3√x+7
limx→∞
	√x+2 + √x+3

Jack: @jc wtedy mnozymy

	√x+2 + √x+3
*		*
	√x+2 + √x+3

	3√(x+5)2 − 23√(x+5)(x+7) + 3√(x+7)2
	3√(x+5)2 − 23√(x+5)(x+7) + 3√(x+7)2

Jack: oczywiscie minusy w pierwszym wyrazeniu mialy byc*

jc: Można tak, ale po co, skoro od razu widać, że granicą jest zero. Przyjrzyj się!

Macko z Bogdanca: A jak pozbyc sie czegos takiego? Lim (√x²+5x+1−√x²+1) x→−∞

	√2−x=√1−x
Lim
	√−x

x→−∞

	∞
W drugim mysle ze bedzie podobnie tylko wyjdzie		? =1
	∞

Macko z Bogdanca: 2 drugim ma byc − odp kolejno to 1 i 2.5

Jack: moge tak stwierdzic po tym, ze do gory suma pierwiastkow 3−ciego stopnia, na dole suma pierwiastkow drugiego stopnia.

	mala liczba
Zatem gora jest mniejsza od dolu, co nam da		= 0
	duza liczba

Jednakze takie cos mnie nie przekonuje

Macko z Bogdanca: w pierwszym mozna uzyc a²−b² tak?

grthx:

	∞
[		] to przeciez symbol nieoznaczony .
	∞

Macko z Bogdanca: Bo wlasnie nei wiem co mam zrobic z tym −x pod pierwiastkiem wiem ze x→−∞ Czyli to i tak bedzie dodatnie tak?

Jack: @Macko 1) korzystasz znowu z tego samego...

	√(x2+5x+1) + √x2+1
lim (√x2+5x+1 − √x2+1) *		=
	(x2+5x+1) + √x2+1

=

Macko z Bogdanca: No tak, racja, dzieki

jc: Jack, a taki przykład

	3√x+5
limx →∞
	√3x+7−√2x+3

Janek191:

	(x2 + 5 x + 1) − (x2 + 1)
f(x) =		=
	√x2 + 5 x + 1 + √x2 + 1

	5x
=		=
	√x2 +5x+1 + √x2 +1

	5
=
	√1 + 5x + 1x2 + √1 + 1x2

więc

	5
lim f(x) =		= 2,5
	1 + 1

x→∞

Jack: c.d. pierwszego (tam w mianowniku zgubilem pierwiastek, pardon... )

	x2+5x+1 − x2 − 1
... = lim		=
	√x2+5x+1 + √x2+1

	5x
= lim		=
	√x2(1+5/x+1/x2) + √x2(1+1/x2)

	5x
= lim		=
	|x|√(1+5/x+1/x2)+|x|√(1+1/x2)

	5x
= lim		=
	|x|√(1+5/x+1/x2)+|x|√(1+1/x2)

	5x
= lim
	|x|(√(1+5/x+1/x2)+√(1+1/x2))

teraz, skoro x−> − ∞ to |x| "zamienia sie" w − x zatem

	5x		−5
... = lim		=
	(−x)(√(1+5/x+1/x2)+√(1+1/x2))		2

Pewnie pytanie − skad ta dwojka? otoz mamy √1 + i w drugim pierwiastku tez mamy √1 (bo reszta "sie zeruje")

Janek191:

	√2 − x − √ 1 − x		2 − x − (1 −x)
f(x) =		=		=
	√−x		√−x*( √2 − x + √1 − x)

	1
=
	√−x*( √2 − x + √1 − x)

więc lim f(x) = 0, bo lim √−x*(√2 −x + √ 1 − x) = +∞ x→−∞ x→−∞

jc: x<0

	5x
√x2+5x+1−√x2+1 =
	√x2+5x+1+√x2+1

	−5
=
	√1+5/x+1/x2+√1+1/x2

(licznik i mianownik dzielimy przez −x >0)

Jack: @jc −> 22:51

	3√x+5 * (√3x+7 + √2x+3)
... = lim		=
	x+4

	3√x(1+5/x)) (√x(3+7/x) + √x(2+3/x)
= lim		=
	x+4

	x1/3*√(1+5/x) * (x1/2(√3+7/x + √2+3/x))
= lim		=
	x(1+4/x)

	x5/6*√(1+5/x) * (√3+7/x + √2+3/x)
= lim		=
	x1(1+4/x)

	√(1+5/x) * (√3+7/x + √2+3/x)
= lim		= 0
	6√x(1+4/x)

Jack: Wracajac do macka... Drugi przyklad (post 22:42) jaki tam jest znak pomiedzy ?

	√2−x ± √1−x
lim (
	√−x

x−>− ∞

Janek191: Pewnie + ja zrobiłem dla − .

Macko z Bogdanca: −

Jack: no to masz rozwiazanie Janka post 23:03

Macko z Bogdanca: Super,dzieki! Jack @Janek191 Musiales sie gdzies rabnac post 23.03 tam odpowiedz ma wynosic 1

Macko z Bogdanca: chyba ze jakis blad w ksiazce

Macko z Bogdanca: chociaz u Ciebie wydaje mi sie ze jest wszystko ok...

nick: jak nie jestes pewien to wpisz do wolphrama

nick: lim x to inf (wyrażenie)

Macko z Bogdanca: Ok dzieki, za wskazowke I pozostalym za poswiecony czas.

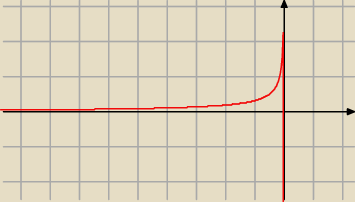
Janek191: Patrz na wykres funkcji f