okrąg opisany i wpisany bas890: Mam jeszcze problem z jednym zadaniem W trójkącie prostokątnym jedna z przyprostokątnych jest dwa razy krótsza od przeciwprostokątnej . Oblicz stosunek pola koła wpisanego w ten trójkąt do pola koła opisanego na tym trojkącie. Proszę o pomoc

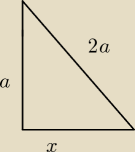kaś: z twierdzenia Pitagorasa x²=a²+(2a)² x=√3a promieN okrEgu opisanego R=połowa przeciwprostokątnej

	2a
R=
	2

	a+b−c
promień okręgu wpisanego r=
	2

	2a
pole dużego koła=π(		)2
	2

	a+a√3−2a
Pole małego koła = π(		)2
	2

	a2(1+√3−2)   4		(√3−1)2		4−2√3
stosunek =		=		=		=1−12√3
	a2		4		4

bas890: nie wim tylko jak obliczyc to małe koło skąd wyszedł taki wynik jak a2(1+√3−2)/4? może ktoś mi to wyjaśnić bardzo proszę