Wykaż
Izydor: 1. Udowodnij, że dla każdej liczby rzeczywistej x prawdziwa jest nierówność x
4−x
2−2x+3>0
2. Wykaż, że dla każdej liczby całkowitej k liczba k(k+1)(k+9)(k
2+1) jest podzielna przez
5.
Czy da się w tym zadaniu w jakiś w miarę sensowny sposób doprowadzić do postaci
przedstawiającej 5 kolejnych liczb całkowitych?
| | 9x4+1 | |
3. Wykaż, że dla dowolnej liczby x∊R \ {0} zachodzi nierówność |
| ≥6 |
| | x2 | |
| | a | | b | |
4. Wykaż, że jeżeli a>b≥1, to |
| < |
| |
| | 2+a3 | | 2+b3 | |
5. Dane jest równanie |mx|+|m|=4, w którym x jest niewiadomą. Dla jakiej wartości
parametru m równanie ma rozwiązania?
| | 4 | |
Tutaj spotkałem się z wyłączeniem |m| przed nawias i otrzymaniem |m|(|x|+1)=4⇒|m|= |
| . |
| | |x|+1 | |
Nie do końca wiem jednak co robić dalej ponieważ próbując rozwiązywać to dalej i zakładając,
że |x|+1≥0 niewiele mi dało.
Będę wdzięczny za pomoc z którymkolwiek z zadań.
17 wrz 20:54
grthx: Zadanie nr 3
PO pomozeniu obu strn przez x2
9x4+1≥6x2
9x4−6x2+1≥0
(3x2−1)2≥0
napisz komentarz
17 wrz 21:02
Benny: zad 4
| | x | |
Pokaż, że funkcja f(x)= |
| jest malejąca dla x≥1 |
| | 2+x3 | |
17 wrz 21:03
Omikron: 1.
Niech f(x)=x4−x2−2x+3
f'(x)=4x3−2x−2
Miejscem zerowym jest 1. Dalej Horner.
f'(x)=(x−1)(4x2+4x+2)
Delta drugiego nawiasu jest ujemna, więc jedynym miejscem zerowym jest 1. Z wykresu pochodnej
wynika, że jest to minimum, a z monotoniczności, że dla x=1 funkcja przyjmuje najmniejszą
wartość.
f(1)=1−1−2+3=1
W takim razie dla każdego x∊R f(x)>0
17 wrz 21:06
grthx: Zadanienr 5
| 4 | |
| narysuj wykres tej funkcji i tnij prosta y=|m| i pamietaj ze |m|=m dla m≥0 i |
| |x|+1 | |
|m|=−m dla m<0
17 wrz 21:08
Izydor: Dziękuje wszystkim. Postaram się popracować nad tym 4'tym tak jak radziłeś (Benny) jeśli na nic
nie wpadnę odezwę się znowu − tym razem bardziej precyzyjnie.
17 wrz 21:09
Omikron: 2.
Rozważamy 5 przypadków.
1) k jest podzielne przez 5, w takim razie iloczyn też jest podzielny przez 5
2) k daje resztę 4, czyli k=5n+4
Wtedy k+1=5n+5=5(n+1), czyli całość podzielna przez 5
3) k daje resztę 1, czyli k=5n+1
Wtedy k+9=5n+10=5(n+2), czyli całość podzielna przez 5
4) k daje resztę 2, czyli k=5n+2
Wtedy k2+1=25n2+20n+4+1=25n2+20n+5=5(5n2+4n+1), czyli całość podzielna przez 5.
5) k daje resztę 3, czyli k=5n+3
Wtedy k2+1=25n2+30n+9+1=25n2+30n+10=5(5n2+6n+3), czyli całość podzielna przez 5.
Skoro w każdym możliwym przypadku liczba jest podzielna przez 5, to jest zawsze podzielna przez
5 (dla całkowitego k).
17 wrz 21:10
Izydor: Dziękuję.
17 wrz 21:12
PW: Zadanie 2.
Jeżeli liczba k jest podzielna przez 5, to nie ma czego dowodzić − pierwszy czynnik jest
podzielny przez 5, a więc iloczyn też.
Pozostaje zbadać pozostałe możliwości:
k =5n+1
k=5n+2
k=5n+3
k=5n+4
dla pewnej n∊N.
Być może w każdym z wypadków pokażemy, że jeden z czynników jest podzielny przez 5.
17 wrz 21:22
PW: Omikron, za długo myślałem bez odświeżania

17 wrz 21:23
grthx: Witaj
PW 
17 wrz 21:24
myszka:
1/ x4−x2−2x+3 = (x−1)2(x2+2x+2) +1 >0 dla x∊R
17 wrz 21:25
Benny: Cześć
PW, gdzie się podziewałeś?

17 wrz 21:25
PW: Cześć, rozmyślałem nad sensem i walczyłem o życie.
17 wrz 21:30
grthx: Czyli to jednak wtedy byles Ty

Dobrze ze wrociles

17 wrz 21:32
myszka:
Inny sposób
2/ Można zapisać tę liczbę tak:
k(k+1)[(k−2)(k+2)+5]*[(k−1)+10] =
(k−2)(k−1)k(k+1)(k+2) +10*k(k+1)(k−2)(k+2) +5*k(k+1)(k−1)+15k(k+1) = 5*t , t∊C
bo liczba (k−2)(k−1)k(k+1)(k+2) −−−− jest iloczynem kolejnych liczb całkowitych
zatem jest podzielna przez 5
suma liczb podzielnych przez 5 jest liczbą podzielną przez 5
co kończy dowód
17 wrz 21:35
Izydor: Pewnie będzie to idiotyczne, ale czy w 2 udowodnieniem nie może być po prostu
x4−x2−2x+3>0⇒x4−x2+3>2x? I tak będę korzystać z zapisu takiego jaki zaproponowała myszka
ale warto zawsze wiedzieć więcej niż mniej.
17 wrz 22:27
grthx:
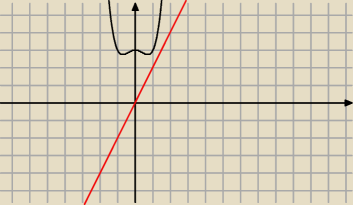
17 wrz 22:47



 Dobrze ze wrociles
Dobrze ze wrociles 
