Równanie logarytm
Maturzysta : | | 1 | |
Log2(9−x2) − |
| Log2 x2 = 3 |
| | 2 | |
Dziedzina to: 9−x
2 >0 więc xe (−3,3) i x
2>0 więc xe (0, +nieskon.)
sumując Dziedzina = (0,3)


Zgadza się ?
16 wrz 13:08
piotr1973: nie ma być (−3; 0)∪(0; 3) bo x2 zawsze jest > 0
16 wrz 13:11
Jerzy:
Nie zgadza się.
16 wrz 13:13
Jerzy:
D = (−3,3)
16 wrz 13:13
grthx:
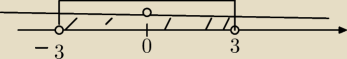
x
2>0 to x∊ℛ|{0}
Popatrz gdzie sie pokrywaja i odrzuc 0
16 wrz 13:14
Jerzy:
Ajjj ...

16 wrz 13:15
Maturzysta : jasne, dzieki !
16 wrz 13:15
grthx: Teraz robisz tak
log
2 (9−x
2)−log
2√x2=3
log
2(9−x
2)−log
2|x|=3
3 sobie zamien na log przy podstawie 2 i mozesz wtedy opuscic logarytmy
16 wrz 13:18
grthx: WItaj
Jerzy 
16 wrz 13:18
Jerzy:
Witam

16 wrz 13:19
prosta:
a można tak?
log2(9−x2)−12*2log2x=3
log2(9−x2)=3+log2x
log2(9−x2)=log22+log2x
9−x2=2x i x∊(−3,0)∪(0,3)
16 wrz 20:33
prosta: poprawka:
9−x2=log28+log2x
9−x2=8x
16 wrz 20:34
prosta: to nie będzie nieeesttety dobrze...
może warto od razu w pierwszym równaniu
po wyznaczeniu dziedziny podstawić x2=t ( próbuję uniknąć wartości bezwzględnej )
16 wrz 21:53
grthx: Dobry wieczor
prosta 
Ja tez nie jestem pewien czy tam ma byc ta wartosc bezwzgledna .
Kolega
Maturzysta jest na forum to moze sie wypowie .
16 wrz 22:03

 Zgadza się ?
Zgadza się ?
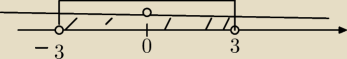 x2>0 to x∊ℛ|{0}
Popatrz gdzie sie pokrywaja i odrzuc 0
x2>0 to x∊ℛ|{0}
Popatrz gdzie sie pokrywaja i odrzuc 0



 Ja tez nie jestem pewien czy tam ma byc ta wartosc bezwzgledna .
Kolega Maturzysta jest na forum to moze sie wypowie .
Ja tez nie jestem pewien czy tam ma byc ta wartosc bezwzgledna .
Kolega Maturzysta jest na forum to moze sie wypowie .