Trapez Gośka: Wykaż, że pole trapezu równoramiennego, którego przekątna o długości d tworzy z podstawą kąt α, jest równe d²sinαcosα. Bardzo proszę o szybką pomoc.

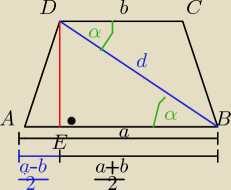
Eta: Ptrapezu = PΔABD + PΔBCD

	a+b
P(trapezu) = 12a*d*sinα + 12b*d*sinα= d*sinα(		)
	2

	a+b
IEBI=
	2

bo w każdym trapezie równoramiennym wysokość h dzieli dłuższą podstawę na odcinki o długościach: IAEI= ^a−b₂ i IEBI= ^a+b₂

	a−b		a+b		a−b+a+b		2a
uzasadniam: IAEI +IEBI= a więc		+		=		=		= a
	2		2		2		2

	IEBI
to: z ΔEBD :		= cosα
	d

	a+b
to IEBI= d*cosα=
	2

wiec P= d*sinα*d*cosα= d²*sinα*cosα c.b.d.o

Gośka: Dziękuje bardzo za pomoc