funkcja wykładnicza Adamek: Dziedziną funkcji f jest zbiór D. Wyznacz zbiór wartości funkcji f, jeśli: a) f(x)=2^−x2+9, D=<−1,1>

	√3
b) f(x)=(		)x2−2x+1, D=<0,3>
	3

Bardzo proszę o pomoc, bo nie wiem jak to zrobić.

Puma: Chyba bedziesz musial rysowac wykresy i odczytac

Karolek:

	512
a) f(x) =		, x≠0
	x2

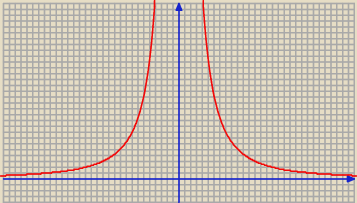
To jest funkcja parzysta, f(−1) = f(1) = 512 ZW_f = (0, 512>

Adamek: W odpowiedzi mam <256,512>

Adamek: Wiem, że muszę najpierw narysować wykres g(x)=−x²+9 i dalej na podstawie niego wnioskować, ale kompletnie nie rozumiem jak

Adam: a) funkcja jest monotoniczna na przedziale [0,1] i jak kolega wyżej zauważył jest parzysta. To, że jest malejąca na przedziale [0,1] łatwo sprawdzić (i trzeba to zrobić). Z tego wynika, że wartość najmniejsza jest dla x=1 lub x=−1, największa zaś dla x=0 b) ów wielomian jest w wykładniku? Niestetety nie potrafię teraz tego rozróżnić

Puma: Moze mialbyc przedzial <−1,0> f(−1)= 2^−(−1)2+9= 2⁸=256 f(0)= 2⁰⁺⁹= 2⁹=512

Adam: w a) dla przedziału [−1,1] jest dokładnie taka sama odpowiedź jak dla [−1,0]. Gwarantuje nam to to, że x występuje tylko w drugiej potędze.

Puma:

√3
	= 3−2/3
3

(3^−2/3)^x2−2x+1= 3^{(−2/3)x2+(4/3)x−2/3}

Puma: I teraz policzyc dla x=0 i x=3 ja tez sie ucze i moge sie mylic .

Adamek: Zrobiłem to tak, że narysowałem wykres g(x)=x²−2x+1 W przedziale <0,3> gmin=g(1), a gmax=g(3) więc liczę f(1) i f(3) i to mój przedział