| √2−1 | |
=(√2−1)2 | |
| √2+1 |
| √2−1 | √2−1 | (√2−1)2 | |||
* | = | =(√2−1)2 | |||
| √2+1 | √2−1 | √22−1 |
 .
.
 |x+y|≤|x|+|y|
Jest to wlasnosc wartosci bezwzglednej i rownosc zachodzi gdy x=y
|y|≤|x−1|
Tutaj musisz rozpatrzryc 4 przypadki
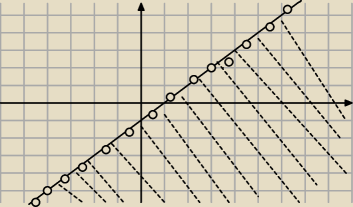
1. y≥0 x≥1 wtedy nierownosc przyjnie postac y≤x−1 (zrobilem rysunek do tego 1 przypadku
wraz z prosta y=x−1
2. y≥0 x<1 wtedy nierownosc ma postax y≤−(x−1)⇒y≤1−x
3. y<0 i x≥1 wtedy nierownosc ma postac −y≤x−1 to y≥1−x
4 y<0 i x<1 wtedy nierownosc ma postac −y≤1−x to y≥x−1
Narysuj te pozostale 3 przypadi i wyznacz czesc wspolna
|x−1|=0 to x−1=0 to x=1 i dlatego rozpatrujemy |x−1| dla x<1 i x≥1
jesli dzielimy lub mnozymyprzez liczbe ujemna to zmieniamy zwort nierownosci (to wiadomo
|x+y|≤|x|+|y|
Jest to wlasnosc wartosci bezwzglednej i rownosc zachodzi gdy x=y
|y|≤|x−1|
Tutaj musisz rozpatrzryc 4 przypadki
1. y≥0 x≥1 wtedy nierownosc przyjnie postac y≤x−1 (zrobilem rysunek do tego 1 przypadku
wraz z prosta y=x−1
2. y≥0 x<1 wtedy nierownosc ma postax y≤−(x−1)⇒y≤1−x
3. y<0 i x≥1 wtedy nierownosc ma postac −y≤x−1 to y≥1−x
4 y<0 i x<1 wtedy nierownosc ma postac −y≤1−x to y≥x−1
Narysuj te pozostale 3 przypadi i wyznacz czesc wspolna
|x−1|=0 to x−1=0 to x=1 i dlatego rozpatrujemy |x−1| dla x<1 i x≥1
jesli dzielimy lub mnozymyprzez liczbe ujemna to zmieniamy zwort nierownosci (to wiadomo