Wyznacz dziedzinę i zbiór wartości funkcji Piwniczanin: Dana jest funkcja f(x)= ctg x + 1/ctg x Rozkładam to na: cos x/sin x + sin x/ cos x= cos² x+ sin² x/(sin x * cos x)= 1/sin*cos dziedzina to ctg x /= 0 sin x/ = 0 cos x/ = 0 Moje pytanie ja wyznaczyć zbiór wartości tej funkcji? Czy wynik <−1;0) u (0:1> jest dobry?

grthx:

1
	= tgx
ctgx

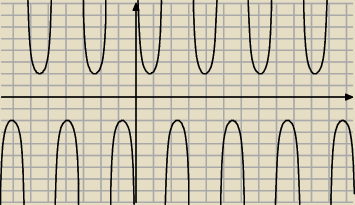
f(x)= tgx+ctgx ten program wygenerowal taki wykres

Jack: @krzysiu, ten program wyswietlil prawidlowa odpowiedz Zw: (−∞ ;−2> U <2;∞)

grthx: Witaj Jack

Jack: Hejo

Mila: D: cosx≠0 i sinx≠0

	π
x≠		+kπ i x≠kπ
	2

	cosx		sinx		cos2x+sin2x		1
f(x)=ctgx+tgx=		+		=		=		⇔
	sinx		cosx		sinx*cosx		12sin(2x)

	2
f(x}=
	sin(2x)

−1≤sin(2x)≤1 jeżeli sin(2x)∊(0,1> to f(x) ∊<2,∞) jeżeli sin(2x)∊<−1,0) to f(x)∊(−∞, −2> Zw_f=(−∞,−2> ∪<2,∞)

Saizou : albo skorzystać z nierówności

	1
a+		≥2 dla a>0
	a

	1
a+		≤−2 dla a<0
	a

Jack: @Milu, jak wyciagasz wnioski, ze jezeli x ∊ to sin jest taki a taki z tego −1 ≤ sin(2x) ≤ 1 i teraz to jakos dzielisz, czy skad to wiesz?

Piwniczanin: Dziękuję Mila, już rozumiem : >

Mila: No pomyśl, Jack

2
	=2
1

2
	=20
110

2
	=2000 000 000
0.000000001

2
	=−2
−1

2
	=−20
−110

2
	=−2000 000 000
−0.000000001

Mila: Sposób Saizou jest bardzo dobry.

Saizou : sin2x jest funkcją ciągła, wiec przyjmuje wartości pośrednie z przedziału [−1,1], w tym przypadku poza 0, bo przez nie nie możemy dzielić

2
	jest największe, gdy dzielimy przez najmniej, czyli przez 0, (a raczej zbliżając
sin2x

się do 0), ale tutaj jest nieciągłość, więc liczymy granice jednostronne (wychodzą +/−∞, czyli końce przedziałów) Zero jest punktem nieciągłości, wiec podzieliło nam przedział [−1,1] na dwa przedziały [−1,0) oraz (0,1]

	2
W przedziale [−1,0) funkcja		przyjmuje największą wartość w −1, czyli −2
	sin2x

	2
w przedziale (0,1] funkcja		przyjmuje najmniejszą wartość w 1, czyli 2
	sin2x

Mila: Powinno być : dla sin(2x)∊[−1,0) i td.

Jack: Kk dzieki

Saizou : skrót myślowy ale słusznie, powinno być sin(2x) € ... itd. O zapis trzeba dbać.