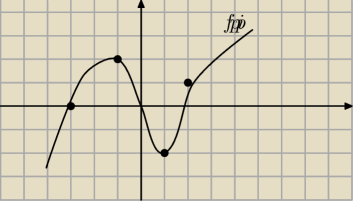
Formułowanie twierdzenia miles: Sformułować twierdzenie o związku między wypukłością (wklęsłością) a znakiem drugiej pochodnej. Korzystając z tego twierdzenia, na podstawie wykresu drugiej pochodnej f00 funkcji f, wyznaczyć przedziały wypukłości (wklęsłości) funkcji f. Zakładamy, że dziedzina funkcji f pokrywa się z dziedziną f'' (Rysunek do najlepszych nie należy robiony na szybko ale : przedstawia funkcję fpp czyli f", punktów nie było w oryginale − dorysowałem, żeby łatwiej można było odczytać) Liczę na pomoc, zależy mi na rozwiązaniu ale wszelki wskazówki mile widziane.

Janek191: Tw: Jeżeli dla każdego x ∊ (a, b) f ''(x) > 0, to krzywa y = f(x) jest wypukła na przedziale (a, b).

Janek191: Tw. Jeżeli dla każdego x∊ (a, b) f ''(x) < 0, to krzywa y = f(x) jest wklęsła na (a, b).