Geometria analityczna
Kolega: Współrzędne wierzchołka trojkata...
Punkty A=(1,−6) i B=(8,2) są końcami przeciwprostokątnej trojkata prostokątnego ABC .
Wierzchołek C należy do prostej o równaniu y=2x i ma ujemne współrzędne . Znajdź współrzędne
punktu C.
Z góry dziękuję

12 wrz 22:21
Jack:
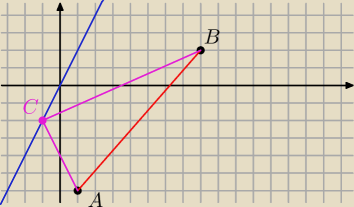
wyglada to mniej wiecej tak
12 wrz 22:24
Saizou :
C(x,2x)
AC
→=[x−1,2x+6]
BC
→=[x−8,2x−2]
AC
→○BC
→=0
[x−1,2x+6]○[x−8,2x−2]=0
(x−1)(x−8)+(2x+6)(2x−2)=0
x
2−9x+8+4x
2+8x−12=0
5x
2−x−4=0
Δ=1+80=81
√Δ=9
| | 1+9 | |
x2= |
| =1 (nie spełnia warunków zadania) |
| | 10 | |
12 wrz 22:37
Kolega: Dzieki dzięki

12 wrz 22:44
Mila:
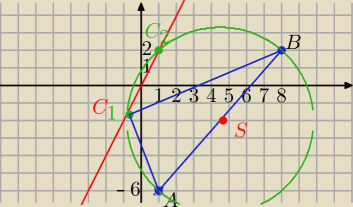
A=(1,−6) i B=(8,2)
C=(x,y), x<0 i y<0
CA
→o CB
→=0 iloczyn skalarny wektorów prostopadłych jest równy 0.
[1−x, −6−y] o [8−x,2−y]=0
(1−x)*(8−x)+(−6−y)*(2−y)=0
(1−x)*(8−x)+(−6−2x)*(2−2x)=0
| | 4 | |
x=− |
| lub x=1 nie odpowiada założeniom |
| | 5 | |
===================
II sposób
| | 1+8 | | −6+2 | | 9 | |
S=( |
| , |
| )=( |
| ,−2) |
| | 2 | | 2 | | 2 | |
|AB|=
√(8−1)2+(2+6)2=
√113
∡C=90
o jako wpisany w okrąg oparty na średnicy
C
1:
C
2:
x=1
y=2 nie odp. zał.
==================
12 wrz 22:53
Kolega: Dziękuję Mila fajny sposób 😍😍
12 wrz 23:02
Mila:

12 wrz 23:07
Saizou :
można też tak:
piszesz prostą AC oraz CB i one mają być prostopadłe
13 wrz 09:23

 wyglada to mniej wiecej tak
wyglada to mniej wiecej tak

 A=(1,−6) i B=(8,2)
C=(x,y), x<0 i y<0
CA→o CB→=0 iloczyn skalarny wektorów prostopadłych jest równy 0.
[1−x, −6−y] o [8−x,2−y]=0
(1−x)*(8−x)+(−6−y)*(2−y)=0
(1−x)*(8−x)+(−6−2x)*(2−2x)=0
A=(1,−6) i B=(8,2)
C=(x,y), x<0 i y<0
CA→o CB→=0 iloczyn skalarny wektorów prostopadłych jest równy 0.
[1−x, −6−y] o [8−x,2−y]=0
(1−x)*(8−x)+(−6−y)*(2−y)=0
(1−x)*(8−x)+(−6−2x)*(2−2x)=0
