funkcje tryg i ich okresowość lucky: Chciałbym prosić o wytłumaczenie jednej sprawy, która dla mnie jest niejasna. Chodzi o okresowość funkcji trygonometrycznych. Może podam przykład. Wydawało mi się intuicyjne, że jeśli zapiszę tak: sin2x = sin(2x + π) to to będzie prawda, bo okres podstawowy sin2x, to π. Ale jak się okazuje to tak nie działa. Chyba należy napisać: sin2x = sin[2(x + π)] = sin(2x + 2π) i w tej postaci rzeczywiście jest okej, co można sprawdzić podstawiając jakieś kąty. Ale jest to dla mnie jakieś dziwne, takie nieintuicyjne, nie rozumiem dlaczego tak należy zapisać. Gdyby ktoś mi rozjaśnił sytuację, będę wdzięczny.

Jerzy: Okresem zasadniczym funkcji sinx i cosx jest 2π

Iryt: y=sin(2x)

	2π
T=
	2

lucky: Jerzy, to ja wiem Rzecz w tym, że nie rozumiem dlaczego dodajemy okres zasadniczy zwykłego sinusa, a nie sinusa podwojonego kąta.

Adamm: sin(2x), okres sinusa jest taki sam jak zawsze f(x)=sin(2x)=sin(2x+2π)≠f(x+2π) widzisz może o co chodzi

lucky: Iryt, chyba nie wiem, co chcesz mi przekazać

lucky: Adamm, właśnie nie widze Jak to okres sinusa jest zawsze taki sam?

Adamm: sinus zawsze będzie miał okres 2π funkcja sin2x ma inny okres ale sam sinus ma okres 2π

lucky: Eh, nie mogę złapać. Bo ja ten zapis: sin2x = sin(2x + π) rozumiem właśnie tak, że do funkcji sin2x dodaję jej okres zasadniczy = π.

Adamm: czyli do sin(x) też byś dodał π?

Adamm: sin(x)≠sin(x+π) więc czemu sin(2x) miałoby się równać sin(2x+π)

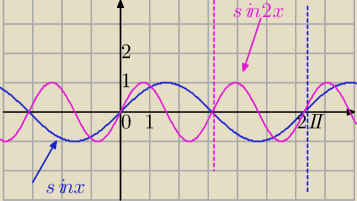
Iryt: y=sinx , T=2π − okres zasadniczy funkcji sinx f(x)=sin(2x)

	T		2π
T1=		=		=π −− okres zasadniczy funkcji sin(2x)
	2		2

2)

	1
y=sin(		x)
	2

T=2π−okres zasadniczy funkcji sinx

	2π		1
T1=		=4π−okres zasadniczy funkcji sin(		x)
	12		2

lucky: "czyli do sin(x) też byś dodał π?" nie, dodałbym 2π "sin(x)≠sin(x+π) więc czemu sin(2x) miałoby się równać sin(2x+π)" wedle mojego niezrozumienia, miałoby się równać sin(2x+π), bo okres sin2x, to π. dalej idąc moim rozumowaniem byłoby, sin3x = sin(3x + 2/3 π), sin4x = sin(4x + π/2) itd. Widzisz teraz czego nie rozumiem?

Adamm: twoje rozumowanie jest błędne, i tyle skoro nie rozumiesz że sytuacja "czyli do sin(x) też byś dodał π?" i sytuacja "sin(x)≠sin(x+π) więc czemu sin(2x) miałoby się równać sin(2x+π) " to dwie i te same, to nie wiem jak dalej mam po prostu ci to powiedzieć

Adamm: skoro do sinx dodajesz 2π to czemu do sin2x dodajesz π ja wiem czemu, ale ja nie rozumiem "czemu" to po prostu nie ma sensu

Iryt: lucky przecież masz podane jak obliczać okres tej funkcji. 16:40 z przykładami. sin(2x)=sin[2(x+π) ] bo T=π sin(2x)=sin(2x+2π) f(x) jest okresowa⇔ f(x)=f(x+T) , T− stała niezależna od x.

lucky: Wiem, że tak się oblicza, ale po prostu tego 'nie czuje' Trudno, może wrócę innym razem do tego. Dzięki wszystkim za poświęcony czas!

Iryt: To wyprowadź wzór z definicji: sin(ax)=sin[a*(x+T)]