zbiór na płaszczyźnie zespolonej jamjest44i4: Narysuj zbiór na płaszczyźnie zespolonej (3+4i)(z−1+i)≤15

	3(i−1)
π/6≤arg		≤π
	z

Rez − Imz ≤2 i to wszystko w klamerce. Od czego zacząć tutaj? Proszę o pomoc

jamjest44i4: wychodzi mi z ostatniego równania x−y≤2 czyi x−2≤y z drugiego trochę głupoty ale 7π/12≥arg z≥π/4 natomiast nie wiem jak zrobić pierwsze równanie. Prawdopodobnie było ono jeszcze w module

Jack: wolfram tez nie wie co z tym pierwszym zrobic...czy to na pewno jest ok (przepisane)?

Adamm: musiało być w module

Mila: Brak modułu w (1). Nie można rozwiązać nierówności między liczbami zespolonymi

jamjest44i4: tak to pierwsze było w module. jak wymnożę to pierwsze wychodzi mi |(3x−4y)+(4x+3y−1)i|≤22 i co z tym dalej? Pozostałe dwa równania są dobrze?

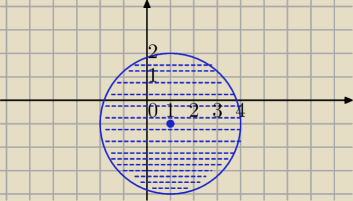
Mila: |z₁*z₂|=|z₁|*|z₂| |(3+4i)(z−1+i)|≤15 ⇔ |3+4i|*|z−(1−i)|≤15 √3²+4²*|z−(1−i)|≤15⇔ 5*|z−(1−i)|≤15 /:5 |z−(1−i)|≤3 koło o środku (1,−1) i r=3

jamjest44i4: Dziękuję bardzo za to rozwiązanie Mila. Czy drugie i trzecie rownanie jest poprawnie rozwiązane?

jamjest44i4: a r nie powinno wyjść √3?

jamjest44i4: z trzeciego równania wychodzi x−2≤y natomiast z drugiego π/6−3π/4≤−arg z +2kπ≤π−3π/4 dla k=0 bo −π≤arg z≤π 7π/12≥arg z≥−π/4

Mila: geometryczna interpretacja liczb zespolonych r=3 http://www.matmana6.pl/tablice_matematyczne/studia/liczby_zespolone/140-definicja_i_interpretacja_geometryczna_liczby_zespolonej Reszta wg mnie dobrze.

jamjest44i4: aa no tak z tym r=3 bo zapomniałem po pierwiastku podnieść drugiej strony. Dziękuję bardzo za odpowiedzi i pozdrawiam

Mila: