Proszę o wytłumaczenie od początku do końca delka: Dwie wysokości trójkąta ABC zawierają się w prostych k: 5x−3y+5=0 oraz l: x+y−1=0. Wiedząc ponadto, że A(−2,1), wyznacz równania ogólne prostych, w których zawierają się boki tego trójkąta.

xd: znajdz proste prostopadle do k i l, oraz podstaw punkt A do nich.

xd: skoro prosta k : 3y = 5x+5

	5		5
y =		+
	3x		3

	3
to prostopadla do niej jest y = −		x + b
	5

podstawiajac punkt A mam :

	6		1
1 =		+ b −>>> b = −
	5		5

stad

	3		1
y = −		x −		(i to jest jeden z bokow trojkata)
	5		5

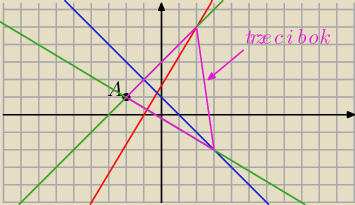
nastepnie prosta l : y = − x + 1 prostopadla do niej to y = x + b podstawiajac punkt A 1 = − 2 + b −>>> b = 3 zatem mamy y = x + 3 Na rysunku proste k i l sa kolorami niebieskim i czerwonym, zielonym kolorem sa proste prostopadle do k i l Widzimy ze proste prostopadle do k i l sa prostymi zawierajacymi dwa boki trojkata. Pozostalo nam znalezc trzeci bok.

xd: chyba cos skopalem...xd

xd: a nie, wszystko sie zgadza

xd: jak widac trzeci bok moze byc gdziekolwiek, byleby byl na rozpietosci zielonych prostych

delka: dziękuje, coś już świta