funkcje
Antonni: To moze ja pierwszy jako przyszly maturzysta
Funkcje f
1 i f
2 sa rosnace w zbiorze R funkcje g
1 i g
2 sa malejace w zbiorze R
Co mozna powiedziec o monotonicznosci podanych nizej funkcji okreslonych na zbiorze R .
Podaj przyklady
a) f
1+f
2
b) f
1−f
2
c) g
1+g
2
d) g
1−g
2
e) a*f
1 gdzie a≠0
f) f
1*f
2
g) g
1*g
2
h) f
1*g
1
i) f
1(f
2(x))
j) f
1(g
1(x))
k g
1(g
2(x))
dziekuje za pomoc
9 wrz 21:36
Jack: a) f1 + f2 = funkcja rosnaca, bo rosnaca + rosnaca to rosnaca : D
niech f1 = x
f2 = x3
zatem funkcja f1 + f2 = x + x3 = x(1+x2) tez jest rosnaca
chociaz nwm czy oto chodzilo : D
9 wrz 21:39
Ajtek:
Włącz myślenie.
9 wrz 21:40
Antonni: Chcialem tak zrobic
dla f1 x1<x2 ⇒f(x1)<f(x2)
dla f2 x3<x4 ⇒f(x3)<f(x4)
Jak to dodac
9 wrz 21:46
Ajtek:
Za bardzo się zagłębiasz w teorię, wyjdź od prostoty tak jak pokazał Jack. Tylko czasami
trzeba będzie pokombinować z różnymi funkcjami.
9 wrz 21:50
Antonni: Ajtek
W zbiorze zadan to zadanie jest z gwiazdka wiec trudne i myle ze trzeba chyba bedzie korzystac
z tych wzorow na funkcje rosnace i malejace
Jesli pomozesz to bedzie miło .
9 wrz 21:57
Ajtek:
Wg mnie wystarczy tylko myślenie i analizowanie funkcji, ich monotoniczności. A moja pomoc
będzie dokładnie taka sama jak Jacka. Wg mnie szkoda czasu na dowodzenie.
9 wrz 21:59
Antonni: Skoro tak uwazasz to sprobuje cos pokombinowac .
Moze jeszce Pani Eta albo Pani Mila pomoze w miedzyczasie
Dzieki .
9 wrz 22:04
Ajtek:
Miałeś już granice funkcji w +/−
∞
Podpowiedź:
f
1=2x, f
2=x
f
1+f
2=3x ⇒ f. rosnąca
f
1−f
2=x ⇒ f. rosnąca, ale
niech f
1=x, zaś f
2=2x to:
f
1+f
2=3x ⇒ f. rosnąca ale
f
1−f
2=−x ⇒f. malejąca
9 wrz 22:11
Antonni: Dziekuje .
Na dzisiaj mi to wystarczy .
9 wrz 22:16
Ajtek:
I jeszcze jedno pytanie, czy miałeś już pochodne funkcji?
9 wrz 22:17
Antonni: Nie mialem jeszcze pochodnych .
W zbiorze zadan sa zadania z wlasnosci funkcji tzn monotonicznosc , parzystosc i nieparzystosc
, okresowosc ,wykresy
9 wrz 22:21
Mila:
a) suma funkcji rosnących jest funkcją rosnącą
f1:R→R, f2:R→R funkcje rosnące
Dla każdego x1,x2 takiego, że x1<x2 :
f1(x1)<f1(x2) oraz f2(x1)<f2(x2)
(f1+f2)(x1)=f1(x1)+f2(x1)<f1(x2)+f2(x2)=(f1+f2)(x2)
cnw.
przykład ;
f1(x)=2x−5
f2(x)=4x+6
f1(x)+f2(x)=2x−5+4x+6=6x+1 f. rosnąca
c) dowodzisz analogicznie korzystając z definicji f. malejących
9 wrz 22:24
Ajtek:
F[Mila]]
9 wrz 22:26
Mila:
b) f1−f2
Nie można określić jednym zdaniem.
Przykłady
b1) f1(x)=−4x
f2(x)=−2x
(f1−f2)(x)=f1(x)−f2(x)=−4x−(−2x)=−2x − funkcja malejąca
b2)
f1(x)=−4x+5
f2(x)=−8x
(f1−f2)(x)=f1(x)−f2(x)=−4x+5+8x=4x+5 f. rosnąca
b3)
f1(x)=−4x+5
f2(x)=−4x+10
(f1−f2)(x)=f1(x)−f2(x)=−4x+5+4x−10=−5 − funkcja stała
9 wrz 22:30
Antonni: Dziekuje bardzo Pani Milu
9 wrz 22:35
Mila:
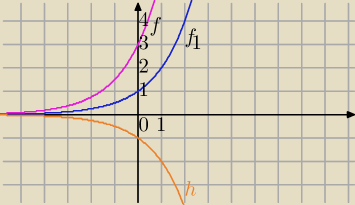
d) podobnie jak (b)
e) a*f
1 gdzie a≠0
f
1( x)− f. rosnąca
dla x
1,x
2∊R⋀ x
x<x
2⇒f
1(x
1)<f
1(x
2)⇔
f
1(x
1)<f
1(x
2) /*a
1)
a>0 wtedy:
a*f
1(x
1)<a*f
1(x
2) ⇔
dla a>0 mamy a*f
1(x)− funkcja rosnąca
2)
a<0 wtedy:
a*f
1(x
1)>a*f
1(x
2)⇔ funkcja malejąca
Przykład :
f
1(x)=2
x
a=3
f(x)=3*2
x− funkcja rosnąca ( możesz wykazać z definicji)
a=−1
h(x)=−1*2
x− funkcja malejąca
9 wrz 22:50
Mila:
Do pozostałych podaj jutro sam swoje obserwacje.
9 wrz 22:51