Planimetria - dowód
lepus: Dany jest trójkąt ABC, na bokach którego obrano takie dwa punkty E i D, że E należy do odcinka
AB, ED=EC oraz D należy do odcinka AC i półprosta ED jest dwusieczną ∡AEC. Udowodnij, że
odcinki BC i ED są równoległe
8 wrz 20:30
Tadeusz:
sprawdź oznaczenia
8 wrz 21:29
lepus: Oznaczenia zgadzają się z treścią zadania
8 wrz 23:31
===:
bez komentarza
9 wrz 08:42
===:
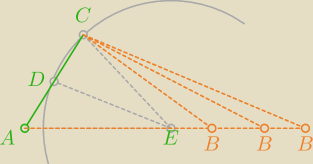
... to które B wybierasz?
9 wrz 09:02
Tadeusz:
na 100% w treści jest |EB|=|EC| a nie |ED|=|EC|
ale skoro trudno porządnie zapisać ...
9 wrz 17:26
Eta:
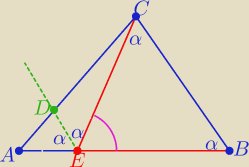|EB|=|EC|
9 wrz 19:40
Tadeusz:
...wrzucił ... znów przed północą sprawdzi
9 wrz 19:42
Eta:
Hej
( zrobiłam już
π..ę 
9 wrz 19:44
grthx: Dobry wieczor
Eta
Szkoda tylko że nie podzielisz się z nią z
pigorem
9 wrz 19:46
Tadeusz:
hej
Ecinka ... a ja dopiero kończę "przetwórstwo" dzikiej róży
Licząc słoiki uświadomiłem sobie, że to w sumie więcej niż dwa solidne wiadra konfitur
i pierwszy słój nastawu na żenichę
9 wrz 19:54
Ajtek:
Bry wieczór. Eta kiedy degustacja?
9 wrz 19:59
Mila:
Ja właśnie warzę powidła z damaszek, chyba za dużo. Konfitury były wcześniej.
Udanych przetworów.
9 wrz 20:00
Mila:
Nalewki dostaję w prezencie.
9 wrz 20:01
Eta:
9 wrz 20:28
Metis:
26 wrz 19:53