pochodna xyz: Styczna do wykresu funkcji f(x)=x³ − 6x² + 12x−4 w punkcie A przecina ten wykres w punkcie B (0,−4) różnym od punktu A a) wyznacz równanie stycznej do wykresu funkcji F w punkcie A A (0,−4)

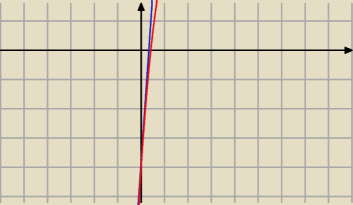
Janek191: f '(x) = 3 x² −1 2 x + 12 a = f '(0) = 12 y = 12 x + b − 4 = 12*0 + b b = − 4 y = 12 x − 4 ========

piotr: y=a*x−4 3x²−12x+12=a y=x³ − 6x² + 12x−4 a=3, x=3, y=5 styczna w punkcie B przechodząca przez A(0,−4): y = 3x−4