zbior wartosci gagatka: F(x)=|x+3|+|x−3|/x wyznaczonych zbior wartości tej funkcji. Próbowałam na funkcję kamerowe i nie wychodzi pomocy

Jack: tak to wyglada?

	|x+3| + |x−3|
f (x) =		?
	x

I trzeba wyznaczyc zbior wartosci? PS co to sa funkcje kamerowe ?

gagatka: Tak to wygląda. Ups słownik w telefonie jak zwykle zrobil robotę.. chodziło o klamerkową

grthx: x+3=0 to x=−3 x−3=0 to x=3 1 przedzial (−∞,−3) 2 przedzial <−3,3) \{0} bo przez 0 nie wolno dzielic 3 przedzial < 3,∞) Wiec narysuj twykres tej funkcji w tych przedzialach

gagatka: Szczerze? Jak na mój rozum to niedokladne to tłumaczenie, ale mimo to dziękuję.

Jack: Nie musi go nawet rysowac. 1) dla x ∊ (−∞ ; −3>

	−x − 3 − x + 3		−2x
f(x) =		=		= − 2 (czyli to jest prosta y=2)
	x		x

2) dla x ∊ (−3;3> \ {0}

	x+3 −x + 3		6
f(x) =		=
	x		x

3) dla x ∊ (3;∞)

	x+3 + x−3
f(x) =		= 2
	x

	6
zatem zbior wartosci to na pewno punkt 2, plus jeszcze zbior wartosci funkcji
	x

oczywiscie w podanym przedziale, to akurat moznaby narysowac, albo poszukac ekstremow, pochodna i te sprawy.

grthx: To znaczy co niedokladne . to jak narysowac to myslalem ze wiesz x∊(−∞,−3) w tym przedziele |x+3|= −(x+3)= −x−3 |x−3|= −(x−3) = −x+3= 3−x Wzorr tej funkcji w tym przedzaile bedzie taki

	−x−3+3−x		−2x
f(x)=		=		= −2
	x		x

tak samo liczysz dla 2 i 3 przedzialu z tym ze dla drugiego odrzucasz 0 bo dostaniesz dzielenie przez 0

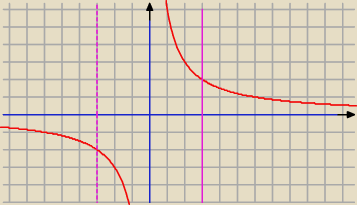
Jack: y = 6/x widzimy, ze w przedziale (−3;3> ma ona zbior wartosci Zw = (−∞;−2) U <2;∞) zatem zbior wartosci calej tej funkcji, (uwzgledniajac f(x) =2) wynosi : Zw = (−∞;−2) U <2;∞)

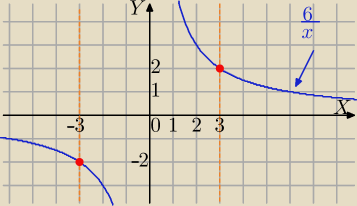
Mila: x≠0 w− wartość funkcji f(x) 1) x<−3

	−x−3−x+3
f(x)=
	x

	−2x
f(x)=		=−2
	x

2) x∊<−3,3)

	6
f(x)=x+3−x+3}{x}=
	x

Zbiór wartości : y<−2 lub y>2 3) x≥3

	x+3+x−3
f(x)=
	x

	2x
f(x)=		=2
	x

(1)∪(2)∪(3) Zw_f=(−∞,−2> ∪<2,∞)

grthx: WItaj Milu Pozdrawiam

Jack: oczywiscie rozw. Mili jest poprawne, gdyz pominalem fakt, ze − 2 tez nalezy do ZW, zatem wynikiem jest rozw. pani Mili

gagatka: Dziękuję! Już znalazłam swój niewyobrażalny błąd.. x−3 potraktowalam jako malejącą i dlatego przedzialy mi nie wychodziły. Głupia ja...

Mila: Witam Panów

Jack: http://jakzdacmaturezmatematyki.pl/zadania/zbior-wartosci-funkcji-matura-r-maj-2014 gdzie ja to widzialem...