Wartość parametru m Qwadrat: Dla jakich wartości parametru m równanie −x² +3x + |x−4| = m ma jedno rozwiązanie? Zrobiłem to i w sumie prawie mi wyszło, tylko że w odpowiedziach jest że ma wyjść m=5, a mi wyszło m=5 i m=0, więc jak sądzę istnieje powód dla którego powinienem odrzucić m=0, tylko ja go nie znam. Jeśli popełniłem jeszcze jakiś błąd to chętnie się dowiem. Moje rozwiązanie: −x² +3x + |x−4| = m Określam dla jakich wartości x, |x−4| przyjmuje wartości nieujemne, a dla jakich ujemne. |x−4|>=0 x−4>=0 x>=4 x∊<4, +∞) 1. x∊(−∞,4) x−4<0, zatem |x−4|=−x+4 −x² +3x −x +4 = m −x² +2x +(4−m) = 0 Δ = 4 +4(4−m) = 4 +16 −4m = 20 −4m Równanie ma 1 rozwiązanie dla Δ=0. 20 −4m = 0 4m = 20 / :4 m = 5 2. x∊<4, +∞) x−4≥0, zatem |x−4| = x−4 −x² +3x +x −4 = m −x² +4x −(4+m)=0 Δ=16 −4(4+m) = 16 −16 −4m = −4m Równanie ma 1 rozwiązanie dla Δ=0. −4m=0 / : (−4) m = 0

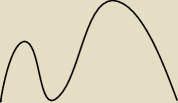
wmboczek: masz górkę niższą i wyższą, tylko na wyższej jest 1 rozw

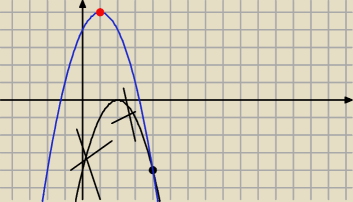
grthx: Jak jest wartosc bezwzgledna to lepiej wedlug mnie robic wykres takiej funkji

Qwadrat: Dobra, chyba rozumiem o co teoretycznie chodzi, ale jak mam to 'fachowo' zapisać?

grthx: Obliczenia sa zrobione ok wedlug mnie . Natomiast twierdze dalej ze w takich wypadkach nalezy zrobic wykres bo zauwaz ze dla m=0 masz 3 rozwiazania Masz miec jedno wiec tylko dla m=5

Qwadrat: Ok, ale jak zrobić ten wykres? To nie jest 'typowa' sytuacja, gdy mogę zrobić tabelkę gdzie dla 'x' obliczam 'y' i sobie rysuję wykres, bo tutaj dochodzi mi jeszcze 'm', a takiego wykresu jeszcze nigdy nie robiłem.

grthx: Napisz jaki jest wzor funkcji z lewej strony tego rownia gdy x≥4 i x<4

Qwadrat: W sensie, że: dla x≥4, f(x)= −x² +3x −x +4 dla x<4, f(x)= −x² +3x +x −4 ?

Qwadrat: Pomyłka, na odwrót: dla x≥4, f(x)= −x2 +3x +x −4 dla x<4, f(x)= −x2 +3x −x +4

grthx: Zreszta masz napisane w swoim poscie jakie to wzory Rysujesz w tych przedzialach i po osi OY tniesz prosta y=m wykres i patrzysz gdzie jedno rozwiazanie jesli tego dalej nie rozumiesz to moze ktos inny sprobuje wytlumaczyc

Adamm: tak, teraz narysuj

Qwadrat: Czyli po uproszczeniu: dla x≥4, f(x)= −x2 +4x −4 dla x<4, f(x)= −x2 +2x +4

piotr: należy sprawdzić czy dla danego m (m=0, m=5), rozwiązanie należy do rozpatrywanego przedziału dla m=5 należy dla m=0 nie należy

Qwadrat: Dobra, narysowałem i wszystko się zgadza, dla f(1) funkcja osiąga maksymalną wartość, równą 5 i tutaj leży prosta y=m. Zastanawiam się tylko, czy wykres tej funkcji wystarczy podpisać jako f(x)?

Mila: Masz takie wzory funkcji dla x≥4, f(x)= −x² +4x −4 dla x<4, f(x)= −x² +2x +4 parabole skierowane w dół. Największa wartość f(x)= −x² +4x −4 w przedziale <4,∞) :

	−4
xw=		=2 ∉<4,∞)
	−2

f(x) jest malejąca dla x≥2 f_max=f(4)=−4 Największa wartość f(x)= −x² +2x +4 w przedziale (−∞, 4):

	−2
xw=		=1∊(−∞, 4)
	−2

f(1)=5 Równanie: −x² +3x + |x−4| = m ma jedno rozwiązanie dla m=5

piotr: rozwiązując zadanie piszesz, że rozpatrujesz funkcję f(x) = −x² +3x + |x−4| i wtedy możesz się posługiwać oznaczeniem f(x)