trojkaty krzysiek: W trapezie o podstawach długości 10 cm i 6cm oraz wysokosci rownej 4cm poprowadzono przekatne, ktore podzielily go na cztery trojkaty. Oblicz pole kazdego z otrzymanych trojkatów

wmboczek: górny i dolny są podobne w skali 5:3 boczne mają równe pola dolny stanowi 5/(5+3) pola połowy trapezu (20)

Eta:

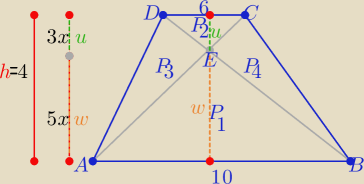
	10		5
Trójkąty ABE i CDE są podobne z cechy (kkk) w skali k=		=
	6		3

	3		5
to u=		i w=
	2		2

	1		5		25
zatem P1=		*10*		=		= 12, 5 cm2
	2		2		2

	1		3		9
P2=		*6*		=		= 4,5 cm2
	2		2		2

	9		25		15
P3=P4= √P1*P2= √		*		=		= 7,5 cm2
	2		2		2

	6+10
lub tak P(trapezu)=		*4= 32
	2

to P₃+P₄= 32 −(P₁+P₂)=32−17= 15 to P₃= P₄= 15:2= 75 cm²

Eta:

	15
Poprawiam ostatni zapis : P3=P4=		= 7,5 cm2
	2