Szkic wykresu. Natka: f(x)=log₂|x−4| Dla jakich wartości parametru a równanie f(x)=a ma dwa pierwiastki różnych znaków ?

Adamm: f(x)=a, |x−4|>0, x≠4 log₂|x−4|=a log₂|x−4|=log₂2^a |x−4|=2^a x−4=2^a lub x−4=−2^a x=2^a+4 lub x=−2^a+4 2^a+4>0, szukamy kiedy −2^a+4<0 −2^a<−4 2^a>4 a>2

Natka: A można szkic jeszcze ?

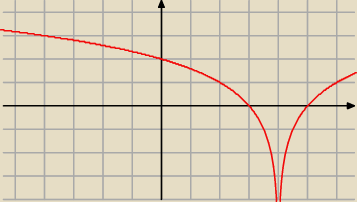
Adamm: narysuj log₂x, zastosuj odbicie na lewą stronę osi y, przesuń o wektor v[4;0]

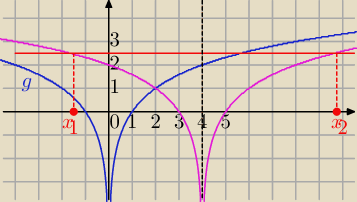
Iryt: Metoda graficzna: 1) g(x)=log₂|x| →T_[4,0]⇒ f(x)=log₂|x−4| f(0)=log₂|2−4|=log₂(4)=2 Równanie f(x)=a ma dwa rozwiązania o różnych znakach dla a>2 Na wykresie przykład dla a≈2.5

Natka: Super, dzięki Myli mi się to odbijanie stąd pytanie o wykres