wykresy funkcji logarytmicznej Soph:

	1
Naszkicuj wykres funkcji f(x) =		log2(x2−6x+9)
	2

Wiem, jak ma wyglądać ten wykres, więc nie chcę gotówców. Prosiłabym żeby ktoś wytłumaczył mi, jak się do tego zabrać.

Adamm:

	1
=		log2(x−3)2=log2|x−3|
	2

Benny: Zauważ, że liczba logarytmowana zwija się do wzoru (x−3)², więc możemy zapisać tak:

	1		1
f(x)=		log2(x−3)2=2*		*log2(x−3)=log2(x−3)
	2		2

Z założeń x−3>0 x>3 Rysujesz więc log₂x i przesuwasz o wektor v=[3,0] i dostajesz log₂(x−3)

Adamm: teraz jest lepiej

Adamm: Benny, źle dla −4 też masz wartość

Adamm: x∊R\{0}

Benny: Eh, myślałem o module i go nie zapisałem

Adamm: zdarza się

Benny: x∊R\{3}

yht: zauważ że x²−6x+9=(x−3)²

	1
f(x)=		log2(x−3)2
	2

skorzystaj z tego, że dla dowolnej liczby a∊R prawdziwa jest równość a² = |a|²

	1
f(x) =		log2|x−3|2
	2

teraz, bez utraty części wykresu, możesz skorzystać z własności log_ab^c=c*log_ab dla b>0

	1
f(x)=		*2log2|x−3|
	2

f(x) = log₂|x−3| i teraz myślę że już sobie poradzisz

	1
Dlaczego nie można było na etapie f(x)=		log2(x−3)2 przerobić funkcję na
	2

	1
f(x)=		*2log2(x−3) ?
	2

Otóż spowoduje to utratę części wykresu dziedzina początkowej funkcji − jest warunek x²−6x+9>0, z tego mamy D=R\{3}

	1
dziedzina funkcji f(x)=		*2log2(x−3) jest już znacznie uboższa, bo mamy x−3>0 czyli x>3
	2

Soph: Dziękuję bardzo za pomoc

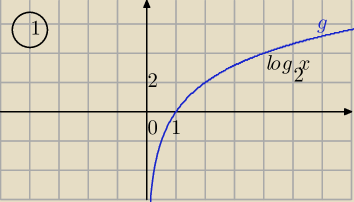
Mila: f(x)=log₂|x−3| wg przekształcenia Adama 1) g(x)=log₂(x)

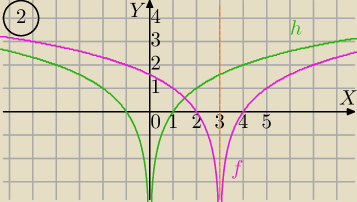
Mila: 2) g(x)=log₂(x)→S_OY⇔otrzymujesz razem h(x)=log₂|x|→T_[3,0]⇒ f(x)=log₂|x−3|